Классическая теория идеального ветряка

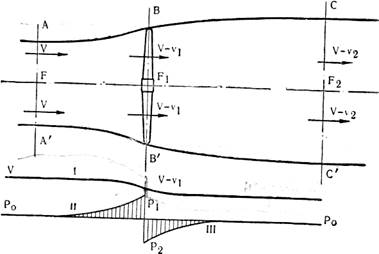Представим равномерный поток ветра, набегающий на идеальное ветроколесо со скоростью V в сечении АА' (рис.1). В сечении ВВ' на ветроколесе скорость будетV₁=V–v₁, а на некотором расстоянии позади ветряка в сечении СС ' скорость будет V₂ = V – v₂.

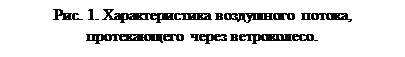При этом вращающееся ветроколесо создаст подпор, вследствие чего скорость потока, по мере приближения к ветряку и некоторое время за ветряком, падает, как показано кривой I на рис. 1

Вместе с этим давление воздуха р, по мере приближения к ветряку, повышается (кривая II), и при прохождении через oметаемую по­верхность оно резко падает. За ветряком образуется не­которое разрежение р₀ – p₂, которое, по мере удаления от ветряка, ассимтотически приближается к нулю, т. е. восстанавливается нормальное давление (кривая III). Потерю скорости за идеальным ветряком можно уста­новить при помощи уравнения Бернулли: 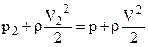. Так как Р₂ < Р₀, то V > V₂.

Кинетическая энергия ветра перед ветряком равна 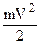, а за ветряком 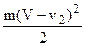. Разность этих энергий затрачена на ветроколесе и, в случае отсутствия потерь, может быть получена как полезная работ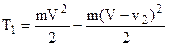а: (а)

Преобразовав правую часть уравнения (а), получим: 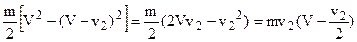. Следовательно: 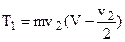(б)

Энергию T₁, воспринятую ветроколесом, можно выра­зить как произведение из силы давления ветра Р на ско­рость в плоскости ветряка (V – v₁), т. е.: T₁= Р(V – v₁). (в)

Лобовое давление P равно приращению количества движения струи, проводящей через метаемую поверх­ность, т. е.: P = m v₂.

Подставляя значение Р в уравнение (в), получим T₁ = mv₂(V – v₁) (г).

Сравнивая уравнения (б) и (г) находим, что: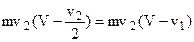

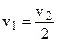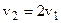откуда: или: (1)

Равенство (1) показывают, что потеря скорости воз­душного потока происходит не только в сечении ветроколеса, но также и на некотором расстоянии за ветряком, причём полная потеря скорости в два раза больше потери на ветроколесе.

Через ометаемую поверхность S ветроколеса протекает масса воздуха m, количество которой за 1 секунду будет равно: m = rSV. (2)

Подставляя значение массы воздуха в выражение кине­тической энергии ветра перед ветроколесом, получим: 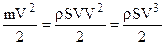. Взяв отношение секундной работы, воспринятой иде­альным ветроколесом: T₁ = P×(V – v_l) к той энергии ветра, которая протекала бы через сече­ние, равное ометаемой поверхности ветряка: ,

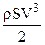получим идеальный коэффициент использования энергии ветра x_i. 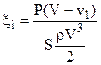(3)

Преобразуем это уравнение: 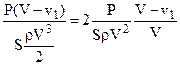Выражение 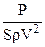называют коэффициентом нагрузки на ометаемую площадь, или коэффициентом лобового давле­ния, и обозначают буквой В, т. е.: 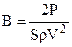(4)

Подставив в это уравнение P = pS(V – v₁)v₂ = pS(V – v₁)2v₁и обозначив 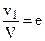, после сокращений получим: 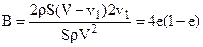(5)

Поступая так же с уравнением (3 66), для x_i. получим: 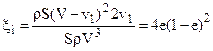(6)

Отношение 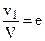называют коэффициентом торможения. Определим значение е, при котором x_i будет иметь максимальную величину. Для этого возьмём первую про­изводную и приравняем её нулю, т. е.: 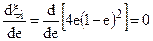или: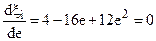

откуда: 3е² – 4е + 1 = 0. Решая это равенство, находим, что x принимает мак­симальное значение, когда e = 1/3, при этом 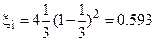Из уравнения (3) находим В – коэффициент нагрузки на ометаемую площадь при максимальном x_i: 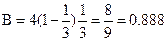Таким образом, из классической теории идеального, ветряка вытекают следующие основные положения.

1. Максимальный коэффициент использования энергии ветра идеального ветроколеса равен x_i = 0,593.
2. Потеря скорости в плоскости ветроколеса равна одной трети скорости ветра:
3. Полная потеря скорости ветра за ветроколесом в два раза больше потери скорости в плоскости ветроко­леса:

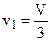
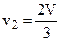
Таким образом, скорость ветра за ветроколесом в три раза меньше скорости ветра перед ветроколесом.

1. Коэффициент нагрузки на ометаемую поверхность ветроколеса равен B = 0,888.

Е.M. Фатеев Задаваясь коэффициентом торможения 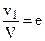в пределах от 0 до 1 и подсчитывая с помощью уравнений (3) и (5), получим следующие значения коэффициентов x_i и В:

Дата добавления: 2015-08-03