Числа и системы счёта

Наверное, необходимо поговорить о числах, они тоже имеют общую единую связь с тетраэдром и тетраксисом, как грани тетраэдра:

Как видим, не только сумма шариков тетраксиса составляет десять, но он также рождает изображения десяти чисел. И на этих числах построена международная десятичная система исчисления человечества. Она называется ещё арабской, но такой не является. Вот символы арабских цифр.

0 1 2 3 4 5 6 7 8 9 10

Основное, что объединяет эти системы исчисления, это десятичность и изобретение «0» для счёта чисел высших порядков. Но десятичная система присутствует и у других народов, корни этих исчислений уходят в глубины тысячелетий. Тогда почему сегодняшняя десятичная система, назовём её международной, так хорошо ложится в структуру тетраэдра? Просто, не только старые традиции, но и современные и будущие системы познания Вселенной связаны с тетраэдром, фундаментальной основой материального мира.

Для полноты понимания чисел, приведу ниже систему счёта в Китае:

1 2 3 4 5 6 7 8 9 10

А вот так выглядит система счёта у древних Майя. Она двадцатеричная, и эта система счёта нарушается только один раз, на втором порядке счёта получается не 20х20=400, а 18х20=360:

Шестидесятеричная система счёта древних Шумер построена на следующих знаках:

И опять шестидесятеричная, но уже Вавилонская система исчисления, которая состоит всего из трёх знаков: единица, десять и ноль. Число определяется местом нахождения знака.

Интересно, почему Шумерская и Вавилонская системы исчисления – шестидесятеричные? Десятеричная – это понятно, удобно считать, когда у человека десять пальцев на руках. И достаточно понятна двадцатеричная система счёта у народов Майя, общая сумма пальцев на руках и ногах у одного человека, равна двадцати. Но что заставило принять шестидесятеричную систему, пока остаётся загадкой. Да и к тому же, она применяется и в сегодняшнем мире, счёт времени секундами и минутами - основан на этой системе счёта. Попробуем ответить, почему так происходит, чуть позже.

Вернёмся ещё раз к правильным многогранникам, хочу особо обратить внимание на то, что их пять. А их грани состоят всего из трёх многоугольников: треугольника, квадрата и пятиугольника (пентагона). Получается парадокс, на плоскости можно построить бесконечное количество правильных многоугольников, а для построения граней пространственных правильных многогранников используется только три. Общая сумма углов у этих трёх многоугольников равна двенадцати, и это не случайность. Самая устойчивая система в пространстве состоит из двенадцати элементов. Это ещё и максимальное количество связей в многоуровневой пирамиде. Двенадцатеричная система счёта используется и для счёта часов в сутках.

Для понимания закономерностей, давайте ещё рассмотрим уровни симметрии в природе. Очень часто симметрия пространства нашей Вселенной стремится к числу три и производных от него шесть, девять, двенадцать, и т.д. Это проявляется на разных уровнях: и в природе - как узоры на цветах, кристаллическая структура воды - снежинки, и в предметах человеческой культуры. Мы говорили уже о фигурах, рождённых равносторонними треугольниками в тетраэдре и о шестиконечной звезде, плюс к этому, вот что ещё дарит нам природа:

Обратимся к следующему типу грани у многогранников - квадрату (четырёхугольнику). Как четырёхугольники, так и четырёхсторонние знаки (кресты), выражают суть симметрии, равной числу четыре, а также более высокому уровню симметрии: восьми, двенадцати и т.д. Как мы уже видели, символы с кратностью четыре, как и три, берут своё начало из тетраэдра. И примеров их реализации существует очень много как в культуре человечества, так и в природе.

Рассмотрим примеры с числом пять. Пятиугольник (пентагон) – третий и последний многоугольник, участвующий в построении правильных многогранников. Пятиугольники и пятиконечные звёзды часто можно увидеть во многих культурах мира. Например, пентаграммы (пятиконечные звёзды) присутствуют в символике разных стран мира. Очень разнообразно пентаграмма также отображена и в природе.

Очень интересный символ выходит, если начать объединять пятиконечные звёзды. Получается картинка, очень похожа на изображение Солнца.

Вот какие замечательные эти три числа: три, четыре и пять. Воистину, их значение раскроется в будущем, во всём своём многоуровневом многообразии. Особо хочу отметить своё предположение, что числа, как счёт материальных объектов нашем мире, получаются не путём складывания единиц, а группируются тройками, четвёрками, пятёрками и числами, им кратными. Любое целое число, большее чем пять, получается путём сложения этих трёх чисел, в любом производном порядке. То есть любой физический процесс будет эквивалентен операциям с этими тремя числами. Например, 37 = 5х5 + 4х3 или 37= 5х6+4+3 и т.д.; 51=5х9 + 3х2 или 51=5+4х10+3х2 и т.д.; 19=5х3 + 4 или 19=5х2+3х3 и т.д.

Вот ещё одно интересное свойство этих трёх чисел. Представим себе две окружности, и пусть одна вращается вокруг другой. На вращающейся окружности поместим «карандаш», который будет рисовать траекторию движения этой окружности. Это называется спирограф. При отношении диаметров, у неподвижной окружности, к вращающейся 5/3 и 5/4, получаются такие вот траектории:

А это траектории при соотношении диаметров: 4/5 и 4/3.

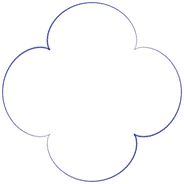
Теперь посмотрим, что у нас получится для соотношения диаметров – 3/4 и 3/5.

Как мы уже чуть раньше заметили, самая древняя система счета - Шумерская, использует шестидесятиричную систему счёта. Теперь попробуем понять, почему. Ответ на этот вопрос лежит в тетраэдре и числах: три, четыре и пять. Всё очень просто, шестьдесят - это первое число, которое делится на три, четыре и пять без остатка.

Тетраэдр - основной кирпичик Вселенной

Рассмотрим подробнее свойства тетраэдра. У него четыре равнозначные вершины, четыре грани и шесть рёбер, он составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Радиус описанной сферы:

Радиус вписанной сферы:

Радиус вписанной сферы, больше ровно на три, радиуса описанной сферы.

Площадь поверхности:

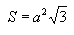
Объем тетраэдра:

Тетраэдр имеет также наименьшее число граней среди всех правильных многогранников, в общем, как и равносторонний треугольник, у которого наименьшее количество сторон и углов, среди всех многоугольников. Каждая вершина, как и грань, соответствует одному из первоэлементов бытия, которые мы условно назовём: огонь, воздух, земля и вода; или север, восток, юг и запад. По сути, фигура трёхгранной пирамиды есть то, что мистики называют Сфинксом, и если мы напишем на каждой грани следующие буквы – ЙОД-ХЕ-ВАВ-ХЕ, то получим – Имя Творца Всего Сущего, Иегова. У этих четырёх древнееврейских букв есть ещё одно название «Тетраграмматон» (в переводе с греческого языка, состоящий из четырёх букв). Очень интересным является наблюдение П.Д.Успенского из книги «Новая модель вселенной»: «Четыре начала, по словам каббалистов, составляют все и вся в мире. Открывая эти четыре начала в вещах и в явлениях совершенно разного порядка, в которых, казалось бы, нет ничего общего, человек обнаруживает подобие этих вещей и явлений друг другу. Постепенно он убеждается, что всё в мире построено по одним и тем же законам, по одному плану. С определённой точки зрения обогащение и рост интеллекта заключается в расширении его способности находить подобия. Поэтому изучение закона четырёх букв, или имени Иеговы, представляет собой могучий способ расширения сознания. Идея совершенно ясна. Если Имя Божества пребывает во всём (если Бог присутствует во всём), то всё должно быть подобно друг другу, самая мельчайшая часть подобна Божеству. Что вверху, то и внизу»

Тетраэдр, с точки зрения геометрии, это трёхмерная пространственная фигура, но как нам её отразить на плоскости для удобной записи в книгах? Разберём детальнее по участкам тетраэдр. Он состоит из четырёх граней, и каждая грань состоит из трёх равных углов. То есть, мы можем построить на плоскости таблицу, у которой будет четыре горизонтальных ряда по три элемента в каждом ряду, и получим прямоугольник три на четыре - матрицу тетраэдра. Посмотрим на неё:

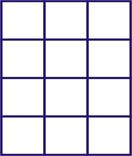
Очень напоминает один из символов неразгаданной древней письменности Хараппской цивилизации (древнейший город Мохенджо-Даро, один из её городов). А также эта матрица очень похожа на церемониальный нагрудник, о котором на горе Синай, Бог рассказал Моисею, и о том, как его изготовить. Церемониальный нагрудник необходимо украшать драгоценными камнями в четыре ряда, по три камня в каждом. Всего получается двенадцать ячеек, следовательно, столько же камней в них. Вот полный текст из библии: «15 Сделай наперсник судный искусною работою; сделай его такою же работою, как ефод: из золота, из голубой, пурпуровой и червленой шерсти и из крученого виссона сделай его;

16 он должен быть четыреугольный, двойной, в пядень длиною и в пядень шириною;

17 и вставь в него оправленные камни в четыре ряда; рядом: рубин, топаз, изумруд, - это один ряд;

18 второй ряд: карбункул, сапфир и алмаз;

19 третий ряд: яхонт, агат и аметист;

20 четвертый ряд: хризолит, оникс и яспис; в золотых гнездах должны быть вставлены они.

21 Сих камней должно быть двенадцать, по числу [двенадцати имен] сынов Израилевых [на двух раменах его], по именам их [и по рождению их]; на каждом, как на печати, должно быть вырезано по одному имени из числа двенадцати колен.»

Тетраэдр находится в любых конструкциях, и его элементы симметрии проявляются на различных уровнях. То есть, он присутствует в построении минимальной частицы бытия, и его структура повторяется и на уровне атомов и молекул, а также на клеточном уровне и на макро-уровнях.

Когда-то в школьные годы, я размышлял, почему в нашем трёхмерном мире все тела: атомы, молекулы, планеты, звёзды – имеют шарообразную форму. Теперь я получил ответ на этот вопрос. Тетраэдры, при объединении друг с другом, приобретают шарообразную форму - это первое, а второе - большинство минералов, составляющих поверхность Земли, состоят из силикатов, молекулярная структура которых укладывается в тетраэдр (в центре кремний, и четыре атома кислорода вокруг него). А самый прочный материал на планете – алмаз, его элементарная ячейка представляет собой тетраэдр, в центре которого и на четырех вершинах расположены атомы углерода. Привожу чуть ниже кристаллическую решётку алмаза - а и углерода - b:

Как мы видим, и в первом, и во втором случае присутствует шестиугольник. Посмотрим на картинку с тетраэдром. На его грани чётко виден шестиугольник, рождённый тетраэдром.

Как много структур в реальном мире повторяет форму шестиугольника! Их количество настолько же многообразно, как и сама жизнь. На перечисление даже небольшой части уйдёт целая вечность. Но о некоторых я расскажу сейчас. Посмотрим на то, как выглядят структуры пчелиных сот, и кристаллов льда - и мы увидим, что это шестиугольники.

Вот что писал Кеплер, в своё время, про это явление природы: «Поскольку … снежинки имеют форму шестиугольной звезды, то на то должна быть определенная причина. Ибо если это случайность, то почему не бывает пятиугольных или семиугольных снежинок, почему всегда падают шестиугольные, если только они от соударений не утрачивают форму, не слипаются во множестве, а падают редко и порознь? Когда я недавно рассуждал с кем-то на эту тему, то мы сошлись прежде всего на том, что причину следует искать не в веществе, а в действующем начале.…Что стоит за шестиугольной формой пчелиных сот? Инстинкт, которым пчелы наделены от природы и который позволяет им строить именно такие соты? Творец, который заложил в соты свои архетипы зодчества?». Похоже, что задача, заданная Иоганном Кеплером, получила своё объяснение. Причиной этого феномена является тетраэдр как первооснова Вселенной, то есть монада - термин, который ввёл ещё Джордано Бруно. Оказывается, он расширил границы человечества не только в макромире, предсказав существование миров, таких же обширных как наша солнечная система, вокруг других звёзд, но и в микромире, предвидя существование монады. Так же очень много сил отдал изучению монады Лейбниц Г.В. Вот некоторые его мысли, взятые из книги "Монадология ": «Итак, можно сказать, что монады могут произойти или погибнуть сразу, т.е. они могут получить начало только путем творения и погибнуть только через уничтожение, тогда как то, что сложно, начинается или кончается по частям. … Я принимаю также за бесспорную истину, что всякое сотворенное бытие – а, следовательно, и сотворенная монада - подвержено изменению и даже что это изменение в каждой монаде беспрерывно».

На фотографиях, показанных ниже, мы видим: северный полюс Сатурна (снимок NASA) и выход на поверхность побережья Ирландии шестиконечных столбов горной породы. На обоих снимках чётко видна шестиконечная структура.

Тетраэдр составляет основу мира. Интересно посмотреть, что говорит математика и физика элементарных частиц об этом. Обратимся к фрактальной геометрии. Это очень модное и перспективное направление в математике. Фрактал (лат. fractus — дробленый) — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Масштабная инвариантность, наблюдаемая во фракталах, может быть либо точной, либо приближённой. Вот так выглядит снежинка Коха.

А это треугольник Серпинского, один к одному выглядит как грань многоуровневый тетраэдр.

Из этих геометрических фракталов самым знаменитым является первый - снежинка Коха. Она строится следующим образом: на каждой из грани равностороннего треугольника убирается центральная часть, потом добавляется два отрезка, такой же длины, как удалённый отрезок. После бесконечного повторения, мы получаем снежинку Коха, фрактал бесконечной длины.

Создание треугольника Серпинского выглядит следующим образом:

И как следствие, после бесконечного числа повторения встраивания треугольников, получится бесконечное число внутренних треугольников в конечном первом треугольнике. Интересно, а не построен ли и наш мир по похожей схеме - мы как встроенные треугольники в теле первичного великого треугольника? Древний философ Платон немного приоткрывает завесу с великой тайны в своей книге «Тимей»: «Различных по величине треугольников было столько, сколько родов различают ныне (внутри основных видов). Сочетание их между собой и с другими треугольниками дало беспредельное многообразие».

Перейдём к физике элементарных частиц. Ниже приведены схемы с барионным и мезонным октетами. Барионный октет (шестиугольник), показывает построение восьми барионов из трёх кварков, а в мезонном октете частицы строятся из одного кварка плюс одного антикварка.

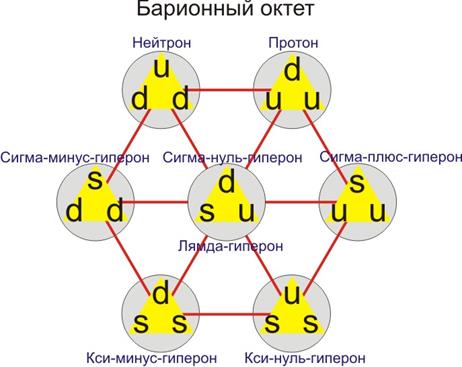
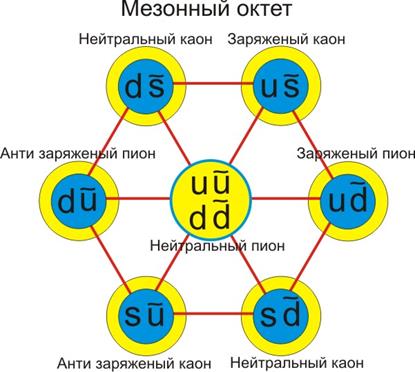
Я не буду углубляться в теорию элементарных частиц, но и тут чётко прослеживается сотоподобная закономерность их систематизации.

Общие законы человеческого познания, проявившиеся в открытиях атомной физики, не являются чем-то невиданным и абсолютно новым. Они существовали и в нашей культуре, хотя гораздо более заметное и важное место всегда занимали в буддийской и индуистской философии. То, что происходит сейчас, - подтверждение, продолжение и обновление древней мудрости».

Дата добавления: 2015-08-02