Влияние локальных неоднородностей в разрезе

Характер влияния неоднородностей на точность определения скоростей зависит от вида неоднородностей, их местоположения в разрезе, их размеров (в сопоставлении с длиной расстановки сейсмоприемников), способа определения V_эф и поэтому в общем виде исследован быть не может.

Рассмотрим частный (но часто встречающийся) случай – влияние высокоскоростной локальной неоднородности (V₂ > V₁) при определении V_ОГТ волн, отраженных от
границы R.

На рисунке приведены:

- лучевая схема для трех ОГТ (А,В и С), где показаны траектории нормальных и крайних лучей;

- графики годографов ОГТ для этих точек;

- графики линий t₀, средней скорости и скорости V_ОГТ

Нетрудно видеть, что лучи, формирующие годограф ОГТ в точке А, не захватывают скоростную неоднородность. Соответственно по этому годографу будет определяться скорость V_ОГТ = V_эф» V_ср .

В точке В центральный луч проходит через центр неоднородности и время t₀ для этого годографа будет меньше, чем для годографа в точке А. Крайний же луч не захватывает неоднородности, следовательно, время прихода волны в крайних точках годографов А и В будет одинаковым, т.е. годограф В будет иметь бóльшую стрелу прогиба, чем годограф А и, соответственно, определенная по нему скорость V_ОГТ будет меньше V_ОГТ в точке А, и тем более меньше средней скорости в точке В.

В точке С лишь центральный луч не попадает в область неоднородности и
t₀(C) = t₀(А), Крайние лучи рассматриваемого годографа проходят через неоднородность, следовательно времена регистрации отраженных волн будут меньше, чем времена в соответствующих точках годографа А, соответственно стрела прогиба годографа С будет меньше стрелы прогиба годографа А и V_ОГТ (С ) > V_ОГТ (A).

Рассмотренный пример показывает, что по поведению параметра V_ОГТ в области скоростной неоднородности (область аномальных значений t₀) трудно судить о характере изменения скоростной характеристики разреза даже в таком простом случае, как рассмотренный выше.

Построение одномерной скоростной модели V_эф

В настоящее время при обработке сейсморазведочных материалов чаще всего определяются скорости V_ОГТ = V_эф / cos j, (10)
т.е. для пересчета V_ОГТ в V_эф надо знать косинус угла наклона отражающей границы.

Для определения угла наклона границы j используется временной разрез.

В точках х₁ и х₂ по исследуемому горизонту в окрестности точки анализа скоростей в определяются времена t_0,1 и t_0,2. (Условие: на интервале определения угла наклона граница должна быть плоской).

Из лучевой схемы видно, что Sin j = (h₂ – h₁) / (x₂ – x₁) = Dh/Dx.

Величины h₁ и h₂ неизвестны, но Dh может быть найдено из разности времён t_0,2 – t_0,1. Если скорость в толще над отражающей границей равна V, то

Dt₀ = t_0,2 – t_0,1 =(2 h₂/V) – (2h₁/V) = (2h₁/V)+ (2Dh/V) – (2h₁/V), откуда: Dh = (Dt₀·V)/2 и, следовательно, Sin j = (Dt₀·V)/2Dx

Из выражения (10)следует, что cos j = V_эф / V_ОГТ и, полагая V_эф » V, можно записать (cos j)² = (V_эф / V_ОГТ)² = 1 – (Dt₀·V)²/(2Dx)², т.е. пересчет V_ОГТ в V_эф может быть выполнен в соответствии с V_эф (11)

Как известно, годограф отраженной волны имеет форму гиперболы только тогда, когда толща пород над отражающей границей однородна и изотропна и сейсмические лучи, соответственно, прямолинейны. Слоистый характер разреза предполагает излом луче на границах раздела и приводит негиперболичному годографу. Скорости, вычисляемые путем гиперболической аппроксимации наблюдённых годографов оказываются зависимыми от их длины, а именно – V_эф возрастает с увеличением длины аппроксимируемого годографа. Максимально близкой к значению V_сред будет предельная эффективная скорость: (12)

Есть ряд зависимостей, связывающих V_е (V_RMS в зарубежной литературе) и V_эф. Достаточно широко используется формула Брауна (Brown):

(13)

где t – нормальное приращение времени на интервале l определения V_эф по годографу
отраженной волны (стрела прогиба годографа);

s – дисперсия пластовых скоростей по отношению к V_сред.

Предельные эффективные скорости пересчитываются в интервальные на основании ранее полученного выражения для V_е: 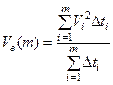, или

Учтём, что:

- t₀(i = 0) = 0;

- ;

-

Тогда: ,

Откуда следует, что

Разрешая полученное равенство относительно интервальной скорости в m -ном интервале получим: (14)

здесь t_0,(m-1), V_e,(m-1) – значения t₀ и V_e на кровле m -ного слоя,

t_0,(m), V_e,(m) – значения t₀ и V_e на подошве m -ного слоя.

Выражение (14) называется формулой Урупова-Дикса и широко используется для пересчета предельных эффективных скоростей в интервальные и, соответственно, построения одномерной скоростной модели исследуемой среды. Ограничением его является то, что исходное выражение для V_e получено в предположении квазигоризонтального залегания слоёв.

Дата добавления: 2015-08-02