Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Минимизация системы Булевых функций

Типовые логические элементы и их обозначения на функциональных схемах. | Типы логических систем. | Задачи анализа и синтеза комбинационных схем. | Построение комбинационных схем (КС) по минимальным нормальным формам в различных базисах. | Задача факторизации (факторного преобразования) булевой функции. | Оценка эффекта факторизации. | Факторизация системы Булевых функций | Декомпозиция системы Булевых функций |


Читайте также:
  1. IV. НАЧАЛЬНЫЙ ЭТАП ВОИНЫ. ФОРМИРОВАНИЕ СИСТЕМЫ "ВО-ЕННОГО КОММУНИЗМА".
  2. V КЛАСС. СИСТЕМЫ РАЗРАБОТКИ С ОБРУШЕНИЕМ ВМЕЩАЮЩИХ ПОРОД
  3. А) Системы передачи с простым кодом
  4. А. Назначение и состав системы
  5. агрузка личной информационной системы
  6. азграничение доходов между бюджетами бюджетной системы РФ.
  7. азработка системы взаимосвязанных аналитических показателей.

 

Задача минимизации применительно к системе Булевых функций решается аналогично как для одной функции и сводится к получению минимального покрытия. Для решения этой задачи система приводится к одной функции путем дополнения множества агументов подмножеством вспомогательных переменных, с помощью которых выделяются отдельные функции системы. Количество вспомогательных переменных k³log2m, m - количество функций.

Пример:

 

 

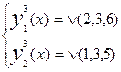
Раздельная минимизация:

 

y1 Cmin (y1)=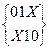

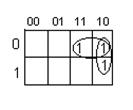
y2 Cmin (y2)=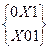

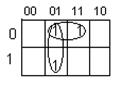
МДНФ: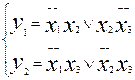

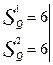
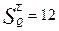
При построении схемы по этому выражению, она разлагается на две независимые подсхемы, отдельные для реализаций каждой функции.

 

Дата добавления: 2015-08-02; просмотров: 76 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Декомпозиция булевых функций.| Совместная минимизация
mybiblioteka.su - 2015-2024 год. (0.006 сек.)