Глава 5. Математическая интерпретация обучения персонала ОрВД на диспетчерском тренажере.

Системы, предназначенные для обучения на диспетчерском тренажере, диагностируют и отлаживают поведение обучаемого и являются динамическими. Поэтому для выбора оптимальной стратегии обучения на диспетчерском тренажере используются математические методы.

Под оптимальной стратегией системы обучения на диспетчерском тренажере понимается выбор отдельных учебных вопросов для изучения в конкретный момент времени t. Таким образом, задача сводится к формированию оптимальной структуры обучения на диспетчерском тренажере.

Каждый конкретный вариант структуры оценивается набором показателей Y = (Y₁…Y_m). Набор показателей Y варианта структуры С зависит от набора параметров Х_С элементов z, составляющих С. Как правило, для каждого показателя Y_i (i = 1,m) можно указать направления желательного изменения и допустимые пределы изменения.

Если желательно увеличение (уменьшение) показателя Y_i, то такой показатель называется максимизируемым (минимизированным). Любой максимизируемый показатель 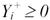можно преобразовать в минимизируемый положительный, например, если взять Y_i = Y_{i MAX}⁺ - Y⁺ _i, где Y_{i MAX}⁺ - достаточно большое число, или Y_i = 1/Y_i ⁺.

В дальнейшем будем считать, что все показатели минимизируемые и положительные.

Обычно в задачах проектирования вводят допустимые значения каждого показателя Y_{i БМП}, причем Y_i Y_{i БМП}, i = 1, m.

Удобно ввести нормированные показатели у_i = Y_i/Y_{i БМП}.

Тогда, поскольку y_iБМП = 1, ограничение технического задания можно записать в виде:

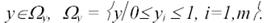(1)

Отношение предпочтения обучающего на множестве можно выразить с помощью целевой функции F(у), которая должна удовлетворять основному требованию: если набор лучше набора , то и наборы и 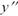считаются равноценными.

Таким образом, целевая функция позволяет создать совершенный квазипорядок на множестве допустимых вариантов проектируемого объекта.

Общую постановку задачи выбора оптимальной структуры можно разделить на две части. В первую входит целевая функция F (у) совместно с множеством , т.е. пара

, (2)

которая определяется отношением предпочтения для всех значений у, поскольку заведомо предпочтительней .

Во второй части общей постановки должно быть задано множество альтернативных вариантов структуры объекта, причем для каждого варианта должны быть определены:

1) функциональные зависимости у = fc(XC), где Хс – вектор параметров элементов, составляющих структуру с;

2) ограничения на Х_С, вытекающие из физических или других объективных законов и определяющие область W_С допустимых значений Х_С, т.е.

. (3)

Для каждого варианта структуры совокупность данных формул может рассматривать как задачу отыскания вектора Х_С*, доставляющего экстремальное значение целевой функции F (f_C(X_C));

. (4)

Тогда задачу оптимизации структуры можно сформулировать как задачу отыскивания подмножества М* множества М:

(5)

Таким образом, задача оптимизации структуры состоит в том, чтобы для каждого варианта структуры определить и зафиксировать оптимальное значение набора параметров Х_С*, а затем выбрать варианты структуры с наименьшим значением целевой функции.

Показателями структуры обучения на диспетчерском тренажере являются объем нормативного материала по отдельной группе вопросов, важность этой группы вопросов для решения главной задачи обучения на диспетчерском тренажере, а также уровень знаний обучаемого по этой группе вопросов, т.е. желательно было бы научить его в первую очередь тем вопросам, которые имеют наибольшую важность.

Данная модель структуры системы обучения на диспетчерском тренажере позволяет добиться следующего интеллектуального поведения системы обучения.

Сначала изучаются наиболее важные вопросы, характеризующие также наименьшим объемом учебного материала, причем возможно повторное обучение одного и того же вопроса.

По мере роста знаний обучаемого происходит переход к изучению других вопросов обучения на диспетчерском тренажере. Возможен возврат к изучению ранее пройденного материала через некоторое время.

Таким образом, разработанная модель системы обучения на диспетчерском тренажере позволяет добиться учета индивидуальных особенностей диспетчера УВД при организации тренажерной подготовки.

Дата добавления: 2015-08-02