Определенный интеграл.

Пусть на отрезке задана функция (рис. 1). Разобьем отрезок на элементарных отрезков точками 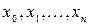, где 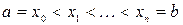. На каждом отрезке разбиения выберем некоторую точку и положим 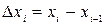, где .

Рис. 1.

Сумму вида будем называть интегральной суммой для функции на отрезке .

Обозначим через максимальную из длин отрезков , т.е. .

Определенным интегралом от функции на отрезке называется предел интегральной суммы при 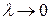, т.е. , 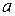- нижний предел, 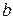- верхний предел, - подынтегральная функция, - подынтегральное выражение.

Замечание 1. Переменную под знаком интеграла можно обозначать любой буквой: 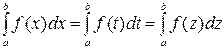и т. д.

Замечание 2. В отличие от неопределенного интеграла 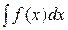, который представляет семейство функций (первообразных), определенный интеграл есть определенное число.

Теорема (достаточное условие существования определенного интеграла). Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.

Свойства определенного интеграла:

1) Постоянный множитель можно выносить за знак интеграла: .

2) Интеграл от алгебраической суммы 2х функций равен такой же сумме интегралов от этих функций: .

3) При перестановке пределов интегрирования знак определенного интеграла меняется на противоположный: .

4) Если пределы интегрирования равны 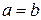, то интеграл равен нулю: .

5) Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей: .

6) Если на отрезке , где , , то и 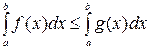, т.е. обе части неравенства можно почленно интегрировать.

7) Если на отрезке , то .

8) Если интегрируема на отрезке , то .

9) Теорема о среднем. Если функция непрерывна на отрезке , то найдется такое значение , что . Т.о. теорема о среднем утверждает, что найдется такая точка из отрезка , что площадь под кривой равна площади прямоугольника со сторонами и .

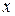Пусть - непрерывная на отрезке функция, а - ее первообразная. Рассмотрим определенный интеграл , где . При изменении меняется и определенный интеграл , т.е. он является функцией верхнего предела интегрирования 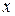, которую обозначим через : 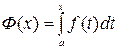. Функция называется интегралом с переменным верхним пределом (с открытым верхним пределом).

Теорема. Если функция непрерывна на отрезке , то функция так же непрерывна на .

Теорема о производной интеграла по верхнему пределу. Пусть функция непрерывна на отрезке . Тогда в каждой точке 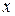отрезка производная функции по переменному верхнему пределу равна подынтегральной функции на верхнем пределе, т.е. .

Теорема. Пусть функция непрерывна на отрезке и 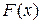- любая первообразная для на . Тогда определенный интеграл от функции на отрезке равен приращению первообразной 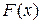на этом отрезке: 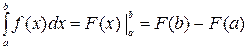- это формула Ньютона-Лейбница или основная формула интегрального исчисления.

Формула Ньютона-Лейбница позволяет находить определенный интеграл, обходя суммирование, при помощи первообразных функций.

Пример. Вычислите и .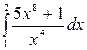

Методы вычисления определенного интеграла:

1. Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть дан интеграл , где функция непрерывна на отрезке . Введем новую переменную равенством , где: 1) между переменным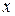и и существует взаимно-однозначное соответствие; 2) непрерывна на отрезке ; 3) ; 4) непрерывна на . Тогда .

Пример. Вычислите .

2. Интегрирование по частям. Теорема. Пусть функции , имеют непрерывные производные на отрезке . Тогда имеет место равенство: 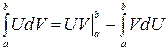- эта формула называется формулой интегрирования по частям для определенного интеграла.

Пример. Вычислить .

Геометрические приложения определенного интеграла:

1. Площадь плоской фигуры.

А) Пусть на отрезке задана неотрицательная функция . Тогда площадь криволинейной трапеции, ограниченной кривой , прямыми 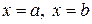и осью абсцисс (рис. 2) численно равна определенному интегралу от функции на , т.е. .

Рис. 2.

Пример. Найти площадь фигуры, ограниченной линиями .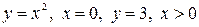

Б) Если функция неположительная и непрерывна на отрезке (рис. 3), то площадь над кривой на отличается знаком от определенного интеграла , т.е.

Рис. 3.

Пример. Найти площадь фигуры, ограниченной кривой и осью абсцисс.

В) Теорема. Если на отрезке заданы непрерывные функции и такие, что (рис. 5).

Рис. 5.

Тогда площадь фигуры, заключенной между кривыми и на отрезке , вычисляется по формуле: .

Пример. Найти площадь фигуры, ограниченной линиями: .

2. Объем тела вращения:

А) вокруг оси : .

Б) вокруг оси : .

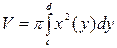3. Вычисление длины дуги кривой на отрезке : .

4. Вычисление площади поверхности вращения вокруг оси : .

Экономический смысл определенного интеграла. Пусть функция описывает изменение производительности некоторого производства с течением времени. Тогда объем продукции , произведенной за промежуток времени , равен .

Физические приложения определенного интеграла:

1. Пройденный путь. Пусть точка движется вдоль некоторой кривой со скоростью . Тогда путь , пройденный точной за время 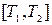, равен .

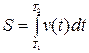2. Масса отрезка. Пусть – плотность распределения массы на отрезке . Тогда масса отрезка равна: .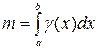

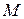3. Работа переменной силы. Пусть под действием некоторой силы материальная точка движется по прямой в направлении оси из точки в точку . Тогда работа, произведенная силой при перемещении точки 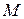из положения в положение равна .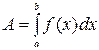

Дата добавления: 2015-08-02