
Читайте также:
|
Неопределенный и определенный интеграл
Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке
на промежутке  , если в каждой точке этого промежутка
, если в каждой точке этого промежутка  .
.
Пример. А)  является первообразной для
является первообразной для 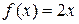 , т.к.
, т.к. 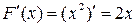 . Б)
. Б)  является первообразной для
является первообразной для 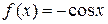 , т.к.
, т.к. 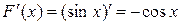 .
.
Если для функции  существует первообразная
существует первообразная  , то она не является единственной. Например, функции
, то она не является единственной. Например, функции 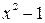 ,
,  и вообще
и вообще 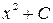 (
(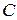 - некоторая произвольная постоянная) являются первообразными для функции
- некоторая произвольная постоянная) являются первообразными для функции 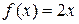 . Таким образом можно сформулировать следующую теорему.
. Таким образом можно сформулировать следующую теорему.
Теорема. Если  и
и  - первообразные для функции
- первообразные для функции  на некотором промежутке
на некотором промежутке  , то найдется такое число
, то найдется такое число 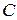 , что будет справедливо равенство:
, что будет справедливо равенство:  .
.
Из данной теоремы следует, что, если  - первообразная для функции
- первообразная для функции  , то выражение вида
, то выражение вида  , где
, где 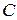 - произвольное число, задает все возможные первообразные для
- произвольное число, задает все возможные первообразные для  .
.
Совокупность всех первообразных функции  на промежутке
на промежутке  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается
и обозначается 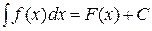 , где
, где 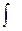 - знак интеграла,
- знак интеграла,  - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение,
- подынтегральное выражение,  - некоторая первообразная для
- некоторая первообразная для  ,
, 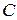 - произвольная постоянная.
- произвольная постоянная.
Операция нахождения неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Данная операция является обратной для операции дифференцирования.
Правила интегрирования неопределенного интеграла:
1) Производная от неопределенного интеграла равна подынтегральной функции, т.е. 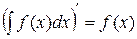 .
.
2) Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. 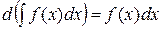 .
.
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.  .
.
4) Постоянный множитель можно выносить за знак интеграла, т.е.  , где
, где  - некоторое число.
- некоторое число.
5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.  .
.
Таблица простейших интегралов
1.  2.
2. 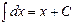 3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8. 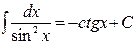 9.
9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14. 
| 15.  16.
16. 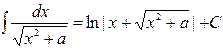 17.
17.  18.
18.  19.
19.  20.
20. 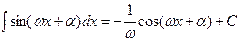 21.
21. 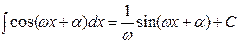 22.
22.  23.
23.  24.
24.  25.
25. 
|
Основные методы интегрирования неопределенного интеграла:
1. Непосредственное интегрирование. Вычисление интегралов с использованием основных правил и таблицы простейших интегралов.
Пример. Найти  .
.
Пример. Найти  .
.
2. Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть функция  определена и дифференцируема на отрезке
определена и дифференцируема на отрезке  , а
, а  - множество значений этой функции, на котором определена функция
- множество значений этой функции, на котором определена функция  . Тогда если
. Тогда если 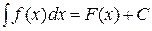 , то получаем
, то получаем  или
или  .
.
Пусть заданный интеграл  не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную
не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную  :
:  . Тогда
. Тогда  ,
,  , т.е.
, т.е.  .
.
Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному.
Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала).
Теорема. Пусть  некоторая первообразная для функции
некоторая первообразная для функции  . Тогда если вместо аргумента
. Тогда если вместо аргумента 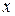 подынтегральной функции
подынтегральной функции  и первообразной
и первообразной  подставить выражение
подставить выражение  , то это приведет к появлению дополнительного множителя
, то это приведет к появлению дополнительного множителя 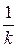 перед первообразной:
перед первообразной:  , где
, где  и
и 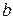 - некоторые числа,
- некоторые числа, 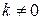 .
.
Алгоритм метода:
1) Делаем замену.
2) Дифференцируем замену  .
.
3) Под знаком интеграла переходим к новой переменной.
4) Находим табличный интеграл.
5) Возвращаемся к старой переменной.
Пример. Найти  .
.
3. Метод интегрирования по частям. Метод основан на теореме: Пусть функции  и
и  определены и дифференцируемы на промежутке
определены и дифференцируемы на промежутке  , и функция
, и функция  имеет первообразную на этом промежутке. Тогда функция
имеет первообразную на этом промежутке. Тогда функция  также имеет первообразную на промежутке
также имеет первообразную на промежутке  , причем справедлива формула
, причем справедлива формула  . Учитывая, что
. Учитывая, что 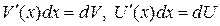 , получим
, получим  .
.
Интегрирование по частям состоит в том, что подынтегральное выражение  представляется каким-либо образом в виде произведения двух множителей
представляется каким-либо образом в виде произведения двух множителей  и
и  (последний обязательно содержит
(последний обязательно содержит  ) и согласно формуле данное интегрирование заменяется двумя:
) и согласно формуле данное интегрирование заменяется двумя:
1) при отыскании 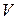 из выражения для
из выражения для  ;
;
2) при отыскании интеграла от  .
.
Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Замечание. За  нужно брать то, что после дифференцирования упрощается.
нужно брать то, что после дифференцирования упрощается.
Пример. Найти  .
.
Пример. Найти  .
.
Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:
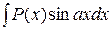
 ,
где ,
где  - многочлен, - многочлен,
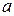 - действительное число - действительное число
| 
|


| 
|

| 
|
4. Интегрирование рациональных функций.
А) Метод неопределенных коэффициентов: Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби 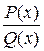 , где
, где  - целые многочлены, причем степень числителя
- целые многочлены, причем степень числителя 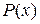 ниже степени знаменателя
ниже степени знаменателя  . Если
. Если  , то справедливо следующее разложение:
, то справедливо следующее разложение:

Для вычисления неопределенных коэффициентов  ,
,  ,
,  обе части тождества приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях
обе части тождества приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях 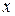 .
.
Пример. Найти 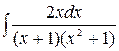 .
.
Б) Метод Остроградского: Если  имеет кратные корни, то
имеет кратные корни, то  , где
, где  - общий наибольший делитель многочлена
- общий наибольший делитель многочлена  и его производной;
и его производной;  ;
; 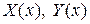 - многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней
- многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней  и
и 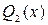 .
.
Пример. Найти  .
.
5. Интегрирование иррациональных функций.
А) Интегралы вида  , где
, где
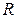 - рациональная функция,
- рациональная функция,  - целые числа, находятся с помощью подстановки
- целые числа, находятся с помощью подстановки  , где
, где  - общее наименьшее кратное чисел
- общее наименьшее кратное чисел  .
.
Пример. Найти  .
.
Б) Интегралы вида  , где
, где  - многочлен степени
- многочлен степени  , полагают равными
, полагают равными  , где
, где  - многочлен степени
- многочлен степени  с неопределенными коэффициентами;
с неопределенными коэффициентами;  - число. Коэффициенты
- число. Коэффициенты  и число
и число  находят с помощью дифференцирования тождества
находят с помощью дифференцирования тождества 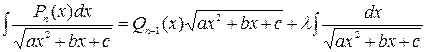 .
.
Пример. Найти 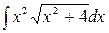 .
.
В) Интеграл вида  с помощью подстановки
с помощью подстановки  приводят к интегралам вида Б).
приводят к интегралам вида Б).
Пример. Найти  .
.
Г) Интегралы вида  , где
, где 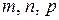 - рациональные числа, выражаются через конечную комбинацию элементарных функций лишь в случаях:
- рациональные числа, выражаются через конечную комбинацию элементарных функций лишь в случаях:
· если  - целое число;
- целое число;
· если 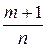 - целое число. Тогда используется подстановка
- целое число. Тогда используется подстановка 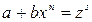 , где
, где  - знаменатель дроби
- знаменатель дроби  ;
;
· если  - целое число. В этом случае используется подстановка
- целое число. В этом случае используется подстановка  .
.
Пример. Найти  .
.
6. Интегрирование тригонометрических функций.
А) Для интегралов вида  , где
, где  - целые числа, возможны случаи:
- целые числа, возможны случаи:
1) Если  - нечетное число, то
- нечетное число, то

Аналогично, если  - нечетное число.
- нечетное число.
Пример. Найти  .
.
2) Если  и
и  четные положительные числа, то подынтегральные выражения преобразуются с помощью формул:
четные положительные числа, то подынтегральные выражения преобразуются с помощью формул:  ,
, 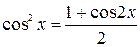 ,
,  .
.
Пример. Найти  .
.
3) Если  и
и 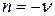 - целые отрицательные числа одинаковой четности, то
- целые отрицательные числа одинаковой четности, то  ,
,
в частности,  ,
, 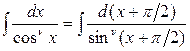 .
.
Пример. Найти  .
.
Б) Интегралы вида  ,
, 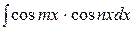 ,
, 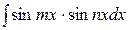 преобразуются с помощью формул:
преобразуются с помощью формул:
 ,
,
 ,
,
 .
.
Пример. Найти  .
.
В) Для вычисления интегралов вида  , где
, где 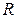 - рациональная функция, можно использовать подстановку
- рациональная функция, можно использовать подстановку  , откуда
, откуда  .
.
Пример. Найти  .
.
Если  , то можно применить замену переменной
, то можно применить замену переменной 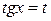 , где
, где  .
.
Пример. Найти 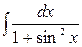 .
.
Дата добавления: 2015-08-02; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача № 9. | | | Определенный интеграл. |