Классы точности средств измерений.

Полная информация о пределах допускаемых основной и дополнительных погрешностей конкретного средства измерений приводится в его техническом описании. Однако для многих распространенных типов средств измерений информацию о пределах допускаемых основных погрешностей можно получить непосредственно из обозначения класса точности.

Класс точности выбирается из ряда (1; 1,5; 2; 2,5; 4; 5; 6)*10ⁿ, где n = 1; 0; -1; -2 и т. д. Класс точности может выражаться одним числом или дробью (если аддитивная и мультипликативная погрешности сопоставимы – например, 0,2/0,05 – адд./мульт.).

Пример 1. Класс точности обозначен одним положительным числом c. Это означает, что для данного средства измерений основная приведенная погрешность γ _о (выраженная в процентах) не превышает по абсолютному значению c %:

, (3.40)

где γ _о,п – предел допускаемой основной приведенной погрешности, Δ_о,п - предел допускаемой основной абсолютной погрешности, X_н – нормирующее значение. Зная X_н, из (3.40) нетрудно найти Δ_о,п ≥ |Δ_о|, где Δ_о – основная абсолютная погрешность средства измерений.

Из (3.40) видно, что для данного средства измерений предел допускаемой основной абсолютной погрешности не зависит от значения измеряемой величины.

Пусть имеется вольтметр, имеющий класс точности 0,5 и диапазон измерений от 0 до 300 В. Для него c = 0,5 и U _н = 300 В. По формуле (3.40)

Δ_о,п = 0,01 cU _н = 1,5 В. Для верхнего и нижнего пределов основной абсолютной погрешности этого вольтметра можно записать: Δ_о,п = ± 1,5 В независимо от его показаний.

Пример 2. Класс точности обозначен так: c/d, где c и d – некоторые положительные числа, причем всегда c > d. Это означает, что для данного средства измерений основная относительная погрешность δ_о (выраженная в процентах) не превышает по абсолютному значению δ_о,п – предела допускаемой основной относительной погрешности, причем

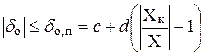, (3.41)

где X – показание средства измерений., а X_к – конечное значение диапазона измерений. Зная X_к и учитывая, что δ_о и Δ_о связаны соотношением

,

получим:

. (3.42)

Из (3.42) видно, что для данного средства измерений предел допускаемой основной абсолютной погрешности линейно возрастает с ростом измеряемой величины X, причем при X = 0 Δ_о,п = Δ_о,п,мин = 0,01 d X_к, а при X = X_к Δ_о,п = Δ_{о,п,макс} = 0,01 c.

Пусть имеется цифровой вольтметр, предназначенный для измерения напряжений постоянного тока, имеющий класс точности 0,5/0,2 и диапазон измерений

от –300 до 300 В. Для него c = 0,5, d = 0,2 и U _к = 300 В. Предположим, что показание вольтметра X = –200 В.

По формуле (3.42) Δ_о,п = 0,01[(0,5 – 0,2)200 + 0,2·300] = 1,2 В. Для верхнего и нижнего пределов основной абсолютной погрешности этого вольтметра при U = –200 В можно записать: Δ_о,п = ± 1,2 В.

В общем случае информацию о пределах допускаемых основных и дополнительных погрешностей нельзя получить непосредственно из обозначения класса точности; необходимо обратиться к техническому описанию конкретного средства измерений, так как нормирование этих погрешностей может осуществляться различными способами.

В качестве примера рассмотрим один из распространенных способов нормирования пределов дополнительной погрешности вольтметров, вызванной выходом температуры окружающего воздуха за пределы нормальной области значений:

Δ_д,п = 0,1·Δ_о,п ·|Θ – 20|, (3.43)

где Δ_о,п и Δ_д,п - пределы основной и дополнительной погрешностей, Θ – температура окружающего воздуха (° C), находящаяся в рабочей области значений.

Дата добавления: 2015-08-02