Формы представления результатов измерений.

В связи со случайностью погрешности Δ результат измерения можно представить в следующем виде:

x; Δ от Δ_н до Δ_в; P, (3.13)

где x – значение измеренной величины; Δ_н и Δ_в – соответственно нижняя и верхняя границы погрешности; P – вероятность того, что погрешность примет значение в пределах от Δ_н до Δ_в:

P = P [Δ_н < Δ < Δ_в]. (3.14)

Интервал [Δ_н; Δ_в] называют доверительным интервалом, а P – доверительной вероятностью.

Обычно выбирают симметричный относительно нуля доверительный интервал, при котором

–Δ_н = Δ_в = Δ_г, (3.15)

где Δ_г – граничное значение погрешности. Тогда (3.14) можно представить в виде

P = P [|Δ| < Δ_г], (3.16)

а результат измерения – в более простом по сравнению с (3.13) виде:

x ± Δ_г, P. (3.17)

При этом задачу оценки точности результата измерения можно было бы сформулировать так: при заданном значении Δ_г необходимо найти P или при заданном значении P найти Δ_г. Очевидно, результат измерения тем точнее, чем меньше Δ_г при заданном P (или больше P при заданном значении Δ_г). В метрологии принято выбирать значения P из ряда: 0,95; 0,99; 1.

Если бы законы распределения погрешностей были известны, то доверительную вероятность можно было бы рассчитать по формулам:

(3.18)

Практически законы распределения погрешностей известны приближенно. Чаще всего их аппроксимируют нормальными законами распределения или законами равномерной плотности.

Для нормального закона распределения погрешностей плотность вероятности

, (3.19)

(где Δ_с = 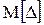– математическое ожидание погрешности),

расчет доверительной вероятности может быть произведен с помощью таблицы функции Лапласа

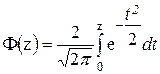(3.20)

по формуле:

(3.21)

При пользовании таблицей необходимо учитывать, что

Если Δ_с = 0 и –Δ_н = Δ_в = Δ_г, то расчет доверительной вероятности упрощается:

. (3.22)

Недостаточной информацией о законах распределения погрешностей объясняется следующая рекомендация: значения Δ_н, Δ_в и Δ_г указываются не более, чем с двумя значащими цифрами, причем последняя значащая цифра должна быть того же порядка, что и последняя значащая цифра результата измерения x. Например,

U = 104,3 В; Δ от –1,2 до 1,5 В; P = 0,95.

Такая запись означает, что для выбранной модели закона распределения погрешностей истинное значение измеряемого напряжения находится в диапазоне от 102,8 до 105,5 В с вероятностью 0,95.

Если систематическая погрешность Δ_с известна, то целесообразно исключить ее из результата измерения, заменив результат измерения x на исправленное значение результата измерения x _испр:

x _испр = x – Δ_с = x + η, (3.23)

где η = –Δ_с – поправка. В отличие от x, исправленное значение x _испр не содержит систематической погрешности и для многих законов распределения погрешностей может быть существенно точнее.

Обычно известно не значение Δ_с, а диапазон возможных значений систематической погрешности:

Δ_сн <Δ_с< Δ_св, (3.24)

где Δ_сн и Δ_св – соответственно нижняя и верхняя границы систематической погрешности. В этом случае поправку рассчитывают по формуле:

(3.25)

Однако после введения такой поправки остаются неисключенные остатки систематической погрешности Δ_сни, причем

< Δ_сни < . (3.26)

При расчете погрешности исправленного результата измерения обычно считают Δ_сни случайной величиной, равномерно распределенной на отрезке, заданном формулой (3.26).

Поскольку определить истинное значение величины в принципе невозможно, т. к. это потребовало бы применения идеально точного средства измерений, то на практике вместо понятия истинного значения величины часто применяют понятие действительного значенияизмеряемой величины, которое настолько точно приближается к истинному значению, что может быть использовано вместо него. Это может быть, например, результат измерения величины эталонным средством измерения.

Дата добавления: 2015-08-02