Простые стрелочные улицы

а) под углом крестовины (рис. 10, а);

б) по основному пути (рис. 10, б).

Несокращенные (простейшие) улицы: а – под углом крестовины; б – то же по основному пути

  l

a)

  l

l

l =e/sinα

б)

Рис. 10.

При расчете стрелочной улицы под углом крестовины определяют значения с, l, Т. Проверяется достаточность вставки f для разгонки уширения колеи. Значения Т, К и f определяются по формулам:

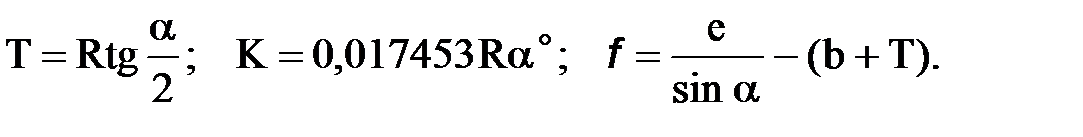
Длина соединительной прямой от торца крестовины до стыка рамного рельса следующего перевода:

Длина стрелочной улицы по проекции от центра первого перевода до вершины угла поворота крайнего пути

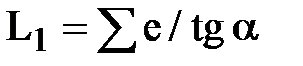
Центр первого перевода принимают за начало координат и, проецируя известные расстояния на ось Х и Y с учетом угла наклона, находят координаты Х и Y центров переводов и вершин углов поворота. Для рассматриваемых точек стрелочной улицы Х=∑e/tgα; Y=∑е. Подсчеты ведут с точностью до 0,001 м.

2. Сокращенные стрелочные улицы имеют более крутые наклоны.

1. Под углом β (не кратным α), по средствам укладки дополнительной кривой после перевода 1 (рис. 11).

Сокращенная стрелочная улица под углом β

Рис. 11.

Сокращенная улица под углом β имеет значительно меньшую длину по сравнению с простыми улицами, поэтому она сокращает длину горловины. Применяются данные сокращенные улицы там, где имеются широкие междупутья.

3. Под двойным углом крестовины (2α) (рис.12).

Сокращенная стрелочная улица под углом 2α

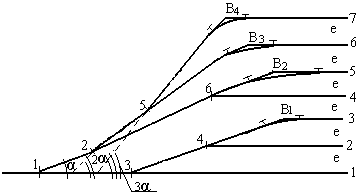
Рис. 12.

Данная стрелочная улица образуется при расположении стрелочных переводов 1, 2, 5, 6 по схеме попутной укладки.

3. Веерные стрелочные улицы имеют ось в виде ломаной линии, направления которой меняется на угол α после примыкания каждого последующего пути. Они применяются в тех случаях, когда из парка необходим выход на основной путь, расположенный к парку под углом более 2α, а также для крайних пучков больших парков. Существует два вида веерных улиц: неконцентрические (рис. 13, а) и концентрические (рис. 13, б).

Веерные стрелочные улицы

a) неконцентрические

б) концентрические

Рис. 13.

а) неконцентрические:

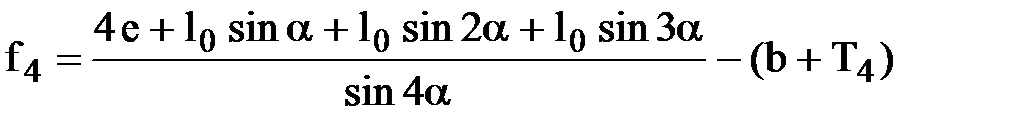
б) концентрические:

В зависимости от сторонности применяемых стрелочных переводов, веерные улицы бывают левосторонними и правосторонними.

Дата добавления: 2015-08-02