Устройство стрелочного перевода

ЗАДАЧА №1

Цель работы: изучить основные размеры стрелочного перевода, виды обыкновенных стрелочных переводов и их применение. Познакомиться с вариантами взаимного расположения стрелочных переводов и научиться рассчитывать расстояние между соседними переводами, уложенных рядом на одном пути.

Задачи практической работы:

Задание 1. Вычертить в масштабе одиночный обыкновенный перевод в осях путей (марку крестовины и тип рельса задает преподаватель);

Задание 2. Вычертить схему заданного стрелочного перевода в рельсовых нитях, указать геометрические размеры в метрах;

Задание 3. По заданной схеме студент должен определить минимальное расстояние между центрами переводов, вычертить ее в масштабе 1:200 и указать основные размеры, привести необходимые формулы для расчета.

Устройство стрелочного перевода

Для соединения путей между собой применяют стрелочные переводы, которые благодаря своей конструкции создают непрерывность рельсовой колеи и позволяют подвижному составу переходить с одного пути на другой.

Основные элементы обыкновенного стрелочного перевода (рис.1):

ü стрелка, включающая два рамных рельса, два подвижных остряка и переводной механизм;

ü крестовина, состоящая из сердечника и двух усовиков;

ü два контррельса, обеспечивающие направление гребней колес в соответствующие желоба крестовины;

ü соединительные рельсовые нити (к которым относится переводная кривая), располагающиеся между концом рамных рельс и началом крестовины;

ü переводные брусья.

При проектировании станций необходимо руководствоваться следующими основными размерами стрелочных переводов, мм:

L_п – полная длина перевода;

m – расстояние от стыка рамного рельса до начала остряка;

а₀ – расстояние от начала остряка до центра перевода;

а – расстояние от переднего стыка рамного рельса до центра перевода:

а = m + а₀;

b – расстояние от центра перевода до торца крестовины:

b = b₀ + q;

b₀ – расстояние от центра перевода до математического центра крестовины;

q – расстояние от математического центра крестовины до ее торца;

α – угол крестовины;

Rпер – радиус переводной кривой по наружной нити.

Центр перевода (ЦП) – это пересечение осей основного и бокового пути.

Математический центр перевода (МЦ) – это вершина угла крестовины α.

Наиболее широкое распространение при проектировании станций получили обыкновенные стрелочные переводы. Они различаются в зависимости от типа рельсов (Р65, Р50 и др.) и марки крестовины, характеризующей ее угол (1/9, 1/11 и др.). Обыкновенные стрелочные переводы бывают правосторонними и левосторонними.

Чтобы в масштабе отложить угол крестовины стрелочного перевода соответствующей марки, рассмотрим отдельно крестовину перевода, рис. 2.

Схема обыкновенного стрелочного перевода

(правостороннего в осях)

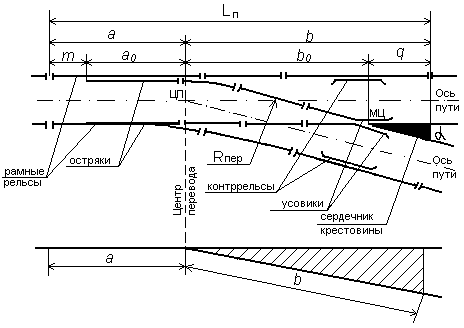
Рис. 1.

Схема сердечника крестовины

В

А О

α

С

Рис. 2.

Из треугольника АВС имеем ВО/АВ = tg α/2, или это отношение ширины к длине. Ввиду малого значения угла α можно принять справедливым равенство 2tg α/2 = tg α. Если принять tg α = 1/N, где N – знаменатель марки крестовины, то получим следующее определение:

отношение ширины сердечника к его длине называется маркой крестовины стрелочного перевода.

Например, марка крестовины 1/9, значит, при ширине крестовины в одну единицу в ее длину должно войти 9 таких единиц (рис.3).

Стрелочные переводы, укладываемые на главных, приемо-отправочных и прочих путях, принимаются в соответствии с типами рельсов для этих путей. Стрелочные переводы на главных путях, по которым пропускаются поезда со скоростью более 100 км/ч, а также одиночные переводы на путях приема и отправления пассажирских поездов (в местах отклонения этих поездов на боковой путь или следования с бокового пути) должны иметь крестовины не круче 1/11. При пропуске пассажирских поездов по прямому пути допускается укладка марки 1/9. На приемо-отправочных путях грузового движения обыкновенные стрелочные переводы укладываются с крестовинами не круче 1/9. Одиночные симметричные стрелочные переводы марки 1/6 обычно укладывают в сортировочных парках в целях сокращения длины их горловин, а также на путях грузовых дворов, локомотивного и вагонного хозяйств.

Примеры построения стрелочных переводов в осях путей:

а – обыкновенный стрелочный перевод; б- одиночный симметричный стрелочный перевод

а)

а ЦП b=9

1/9 h= 1

б)

а ЦП b=6 h= 1

1/6

Рис. 3.

Сторонность стрелочного перевода определяется следующим образом: наблюдатель становится у остряков перевода лицом к крестовине, если переводная кривая отклоняется в правую сторону, то это правосторонний стрелочный перевод, если влево - левосторонний, в обе стороны одинаково – симметричный.

Стрелочные переводы по ходу движения могут быть пошерстными или противошерстными. Если двигаться от остряков к крестовине, то стрелочный перевод будет противошерстным, если от крестовины к острякам – пошерстный.

Дата добавления: 2015-08-02