Условный оператор

1. Ввести три числа. Если они могут быть длинами сторон прямоугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

2. Ввести три числа. Если они могут быть длинами сторон остроугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

3. Ввести три числа. Если они могут быть длинами сторон тупоугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

4. Ввести три числа. Если они могут быть сторонами равностороннего треугольника, вычислить его площадь и длину высоты. Вывести стороны, площадь и длину высоты в порядке возрастания.

5. Ввести три числа. Если они могут быть длинами сторон равнобедренного треугольника, вычислить длины его высот. Вывести длину основания и длины высот в порядке возрастания.

6. Ввести три числа. Если они могут быть длинами сторон разностороннего тупоугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

7. Ввести три числа. Если они могут быть длинами сторон равнобедренного тупоугольного треугольника, вычислить его площадь. Вывести длины сторон и площадь в порядке возрастания.

8. Ввести три числа. Если они могут быть длинами сторон равнобедренного остроугольного треугольника, вычислить его площадь. Вывести длины сторон и площадь в порядке возрастания.

9. Ввести три числа. Если они могут быть длинами сторон разностороннего остроугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

10. Даны координаты трех точек на плоскости. Если они могут быть вершинами остроугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

11. Даны три числа. Если они могут быть длинами сторон треугольника, определить его вид (прямоугольный, тупоугольный, остроугольный). Вычислить длины его высот и напечатать их в порядке убывания.

12. Составить программу, которая определяла бы вид треугольника (равносторонний, равнобедренный, разносторонний, прямоугольный, тупоугольный, остроугольный), если по данным трём отрезкам его можно построить.

13. Даны координаты трех точек на плоскости. Составить программу, которая определяла бы вид треугольника (равносторонний, равнобедренный, разносторонний, прямоугольный, тупоугольный, остроугольный), если данные координаты вершин позволяют его построить.

14. Даны координаты трех вершин прямоугольника. Определить координаты четвертой вершины.

15. Даны три целых числа. Возвести в квадрат отрицательные числа и в третью степень — положительные (число 0 не изменять).

16. Из трех данных чисел выбрать наименьшее.

17. Из трех данных чисел выбрать наибольшее.

18. Из трех данных чисел выбрать наименьшее и наибольшее.

19. Перераспределить значения переменных X и Y так, чтобы в X оказалось меньшее из этих значений, а в Y — большее.

20. Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по возрастанию.

21. Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по убыванию.

22. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения.

23. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной максимальное из этих значений, а если равны, то присвоить переменным нулевые значения.

24. Даны три переменные: X, Y, Z. Если их значения упорядочены по убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.

25. Даны три переменные: X, Y, Z. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.

26. Даны целочисленные координаты точки на плоскости. Если точка не лежит на координатных осях, то вывести 0. Если точка совпадает с началом координат, то вывести 1. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 2 или 3.

27. Даны вещественные координаты точки, не лежащей на координатных осях OX и OY. Вывести номер координатной четверти, в которой находится данная точка.

28. На числовой оси расположены три точки: A, B, C. Определить, какая из двух последних точек (B или C) расположена ближе к A, и вывести эту точку и ее расстояние от точки A.

29. Даны четыре целых числа, одно из которых отлично от трех других, равных между собой. Вывести порядковый номер этого числа.

30. Дан номер некоторого года (положительное целое число). Вывести соответствующий ему номер столетия, учитывая, что, к примеру, началом 20 столетия был 1901 год.

31. Дан номер некоторого года (положительное целое число). Вывести число дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный — 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 — являются).

32. Ввести три числа. Если они могут быть длинами сторон прямоугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

33. Ввести три числа. Если они могут быть длинами сторон остроугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

34. Ввести три числа. Если они могут быть длинами сторон тупоугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

35. Ввести три числа. Если они могут быть сторонами равностороннего треугольника, вычислить его площадь и длину высоты. Вывести стороны, площадь и длину высоты в порядке возрастания.

36. Ввести три числа. Если они могут быть длинами сторон равнобедренного треугольника, вычислить длины его высот. Вывести длину основания и длины высот в порядке возрастания.

37. Ввести три числа. Если они могут быть длинами сторон разностороннего тупоугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

38. Ввести три числа. Если они могут быть длинами сторон равнобедренного тупоугольного треугольника, вычислить его площадь. Вывести длины сторон и площадь в порядке возрастания.

39. Ввести три числа. Если они могут быть длинами сторон равнобедренного остроугольного треугольника, вычислить его площадь. Вывести длины сторон и площадь в порядке возрастания.

40. Ввести три числа. Если они могут быть длинами сторон разностороннего остроугольного треугольника, вывести их в порядке возрастания, вычислить площадь полученного треугольника.

41. Даны координаты трех точек на плоскости. Если они могут быть вершинами остроугольного треугольника, вывести их в порядке убывания, вычислить площадь полученного треугольника.

42. Даны три числа. Если они могут быть длинами сторон треугольника, определить его вид (прямоугольный, тупоугольный, остроугольный). Вычислить длины его высот и напечатать их в порядке убывания.

43. Даны координаты трех точек на плоскости. Составить программу, которая определяла бы вид треугольника (равносторонний, равнобедренный, разносторонний, прямоугольный, тупоугольный, остроугольный), если данные координаты вершин позволяют его построить.

44. Даны координаты трех вершин прямоугольника. Определить координаты четвертой вершины.

45. Даны действительные положительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x и y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия

Циклы

1. Составить программу вычисления суммы вида:

a)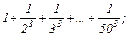

b)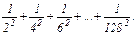

2. Составить программу вычисления при заданных x и a значения функции y вида:

a) ;

b) .

3. Вычислить: ;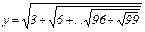

4. Написать программу вычисления при заданном x величины y по формуле

.

5. Вычислить .

6. Составить программу для нахождения и печати всех пифагоровых чисел, не превышающих 20.

7. Дано натуральное n. Вычислить значение выражения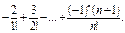

8. Даны натуральное число n и действительное число x. Вычислить:

a)

b)

9. Дано натуральное k. Напечатать k -ую цифру последовательности 12345678910111213…, в которой выписаны подряд все натуральные числа.

10. Вычислить x ₁+ x ₂+…+ x ₂₀, если последовательность x ₁, x ₂, … образована по следующему закону:

1. ;

2. x₁ = 1; x₂ = 0.3; x_i = (i+1) ×x_{i – 2} , i = 3, 4, ….

3. x₁ = x₂ = x₃ =1; x_i = (i+3) × (x_{i – 4} –1)+ (i+4) ×x_{i – 3}, i = 4, 5, ….

11. Дано вещественное число x и натуральное число n. Вычислить .

12. Даны вещественные числа a, h, натуральное число n.
Вычислить , где

13. Дано натуральное число n. Вычислить 1×2+2×3×4+…+ n × …×2 n.

14. При некоторых заданных x, N и E, определяемых вводом, вычислить:

a) сумму N слагаемых заданного вида;

b) сумму тех слагаемых, которые по абсолютной величине больше Е.

Для случая b выполнить суммирование для двух значений Е, отличающихся на порядок, и при этом определить количество слагаемых, включенных в сумму. Сравнить результаты с точным значением функции, для которой данная сумма определяет приближенное значение при x, лежащем в интервале (- R, R).

I) (R=¥).

II) (R=¥).

III) (R=1)

IV) (R=1).

V) (R=1).

VI) (R=1).

VII) (R=1).

VIII) (R=1).

IX) (R=1)

X) 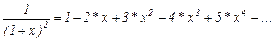(R=1).

XI) (R=1).

XII) (R=1).

XIII) (R=1).

XIV) 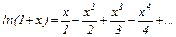(R=1).

XV) (R=¥).

XVI) (R=¥).

Дата добавления: 2015-08-02