Способы определения порядка реакции

1. В способе подстановок подставляют зависимости концентраций от времени в выражение константы реакции предполагаемых порядков. Выбирают уравнение, по которому значение вычисленной константы близко к постоянному значению.

2. В графическом способе изображают зависимости lnc, 1/c или 1/c² от времени при одинаковых начальных концентрациях c₀ всех реагентов. Если зависимости линейны, то реакции описываются уравнениями приведенными выше.

3. По времени t_x, для которого c_x = c₀ · x (здесь непрореагировавшая часть x<1). При одинаковых начальных концентрациях c0 всех реагентов:

t_x = c₀^1-n(x^1-n – 1) / (n-1) · k = A · c₀^1-n (1)

lnt_x = lnA + (1-n) · ln c₀ (2)

(3)

Это уравнение (3) приложимо к реакциям первого порядка. У таких реакций .

4. По скорости в начале реакции. Строят графики зависимости концентрации от времени и построением касательных к 2-3 кривым в один и тот же момент времени определяют скорость реакции при одинаковых начальных концентрациях всех реагентов.

Пусть и . Делением одного выражения скорости на другое исключают константу скорости и после логарифмирования полученного отношения находят n и далее k. Этот способ дает суммарный порядок по всем компонентам.

5. По относительным концентрациям реагентов. Способ по смыслу такой же, что и (4). Только расчеты производят непосредственно с относительными концентрациями r_i = c_i / c₀.

Константы скорости для реакций первого, второго и третьего порядка

Для элементарной реакции (или стадии) первого порядка:

A → Продукты, (1)

или a₁·A₁ + a₂·A₂ →Продукты (2)

выражение для скорости реакции (при порядке по веществу А₂ равном 0):

(3)

Скорость элементарной реакции (1) связана со скоростью образования исходного вещества А соотношением:

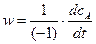, (4)

где (-1) – стехиометрический коэффициент исходного вещества А в уравнении (1).

Подставим (4) в (3):

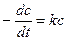(5)

В общем виде скорость формально простой реакции (2) выглядит так:

(6)

Подставим (6) в (3):

, где k`=a₁k (7)

Разделив переменные, получим

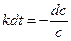(8)

Проинтегрируем выражение в пределах 0 – t и c₀ – c:

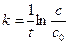, , c = c₀е^-kt (9)

где с₀ – начальная концентрация исходного вещества А;

с – концентрация вещества А к моменту времени t.

Константа скорости реакции 1-го порядка имеет размерность (время)^-1

Пример: с^-1, мин^-1, с^-1.

Время полураспада или полупревращения t_1/2 равно промежутку времени, в течение которого реагирует половина взятого количества вещества.

Из уравнения (9) при с = ½ с₀

(10)

Таким образом, t_1/2 для реакций 1-го порядка не зависит от количества и концентрации исходного вещества и обратно пропорционально скорости реакции.

Степень превращения α – доля распавшегося вещества

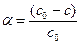(11)

(для реакций 1-го порядка не зависит от начального количества вещества)

Выражение для k можно записать также в виде:

, (12)

где a = с₀ · V – начальное количество вещества

a – x = c · V – количество вещества, которое осталось во всем объеме V к моменту времени t.

х – количество прореагировавшего вещества.

Для элементарной реакции (или стадии) второго порядка:

2A → Продукты (1)

1 случай – реагируют две одинаковые частицы

a₁·A₁ + a₂·A₂ →Продукты (2)

предположим, что по веществу А₂ порядок равен 0.

Тогда (3)

(4)

Подставим (4) в (3) и получим:

, где k=2k^` (5)

Для реакции (2) будет:

(6)

и соответственно

, где k=a₁k^` (7)

Проинтегрируем и получим:

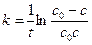(8)

Размерность константы скорости реакции II-го порядка

(концентрация)^-1 · (время)^-1

Пример: л/(моль·с)

Время полураспада (9)

Таким образом, t1/2 обратно пропорционально начальной концентрации исходного вещества.

2 случай – реагируют две различные частицы.

A₁ +·A₂ →Продукты (10)

(11)

(12)

(13)

Учитывая, что с₁ = с₁₀ – х и с₂ = с₂₀ – х уравнение (13) примет вид:

(14)

где с₁₀ и с₂₀ – начальные концентрации А₁ и А₂

х – уменьшение концентрации А₁ или А₂ к моменту времени t.

(15)

Разделим переменные и проинтегрируем:

(16)

Выразим k через степень превращения α:

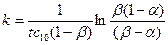(17)

где x = c₁₀ · α и β = с₂₀ / с₁₀

Для элементарной реакции третьего порядка:

3А → Продукты (1)

или A₁ +·A₂ +А₃ →Продукты (2)

1 случай – с₁=с₂=с₃=с в любой момент t:

(3)

(4)

Отсюда и k = 3k` (5)

Для реакции (2) имеем:

(6)

Отсюда и k = k` (7)

Разделим переменные в (5) и (7):

(8)

Проинтегрируем в интервале 0 - t и с₀ - с и получим:

(9)

(10)

Таким образом, t_1/2 для реакции III-го порядка обратно пропорционально квадрату начальной концентрации исходных веществ.

Размерность (время)^-1 · (концентрация)^-2

Пример: л²/(моль² · с)

2 случай – для реакции A₁ +·2A₂ →Продукты (11)

или 2 A₁ +·A₂ →Продукты (12)

при с₁₀=с₂₀=с₀

Для (11) 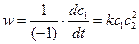(13)

или (14)

Для (12) (15)

или (16)

где х – уменьшение концентрации вещества А₁.

3 случай – для реакции (2) при разных концентрациях веществ А₁, А₂ и А₃:

(17)

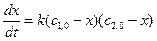или (18)

Кинетика сложных реакций

Большинство реакций являются сложными и состоят из нескольких элементарных стадий.

Основные типы

обратимые (двусторонние) параллельные последовательные

Рассмотрение сложных реакций упрощается, если реакции протекают в стационарных или квазистационарных условиях и имеется лимитирующая стадия. Элементарная стадия называется лимитирующей, когда закономерности всего процесса определяются в основном кинетическими закономерностями этой стадии (другими словами, самая медленная стадия, которая определяет процесс в целом).

Рассмотрим формальную кинетику для сложных гомогенных реакций в закрытых системах.

1. Двусторонние (обратимые) реакции

k₊

А↔B (1)

k_-

где k₊ и k_- - константы скорости прямой и обратной элементарной стадии

w = w₊ - w_- = k₊ · c₁ – k_- · c₂ (2)

где с₁ и с₂ – концентрации А и В в момент времени t/

Учитывая, что с₁ = с₁₀ – х,

с₂ = с₂₀ + х (3)

Получим 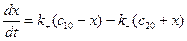(4)

Где с₁₀ и с₂₀ – концентрации А и В при t =0.

В состоянии равновесия w+ = w- и (5)

Заметим, что при наличии двух последовательных двусторонних стадий это положение не очевидно, так как

w₁ w₂

в случае (а) А↔В↔С (6)

w_-1 w_-2

кроме условия равновесия w+ = w-=w₂ - w_-2 можно представить и другие условия. Например, циклическое протекание реакции:

B В

w₁ w_-1 w_-2 w₂ или

w₃

A C А С

w_-3

(б) (в)

Для (б) условие равновесия:

w₁ – w_-1 = w₂ – w_-2 = w₃ – w_-3# 0

Для (в) w₁ = w₂ = w₃ # 0

Принцип детального равновесия. При равновесии в химической реакции любая элементарная стадия протекает с одинаковой скоростью как слева направо, так и справа налево.

Таким образом, обратная реакция в тех же условиях обязательно протекает через те же стадии.

w_-1 w_-2

Отсюда можем записать С↔В↔А (7)

w₁ w₂

В состоянии равновесия

(8)

где х_р – изменение концентрации, которое находят из опыта через достаточно большой промежуток времени после начала реакции, когда система достигает почти равновесного состояния.

(9)

где К – константа равновесия.

Таким образом,

(10)

2. Параллельные реакции

Когда взятое для реакции вещество претерпевает одновременное изменение в двух направлениях и более.

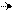
k₁ В

А (1)

k₂ Д

Общая скорость образования вещества А:

(2)

где с₁ – концентрация вещества А.

Разделим переменные и проинтегрируем:

c₁ = c₁₀ · е^-(k1+k2)t (3)

Скорость получения В и Д равна:

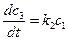и (4)

где с₂ и с₃ – концентрации В и Д.

Подставим (3) в (4) и получим:

dc₂ = k₁c₁₀е^-(k1+k2)tdt (5)

dc₃ = k₂c₁₀e^-(k1+k2)tdt

Проинтегрируем в пределах 0 – с₂ и 0 – с₃:

(6)

3. Последовательные реакции

Промежуточные вещества, которые образуются в одной стадии, расходуются в последующей.

k₁ k₂

А→P→B (1)

k₁

или A→P, w₁ = k₁ · c₁

k₂

P→B, w₂ = k₂ · c₂ (2)

где Р – промежуточное соединение.

Обозначим концентрации А, В и Р через с₁, с₂ и с₃.

1 случай. Скорости обеих реакций примерно одинаковы.

Следовательно, c₁ = c₁₀ · е^-k1t (3)

где с₁₀ – начальная концентрация вещества А.

Скорость образования Р в первой и второй стадиях:

w₁ = k₁c₁ и w₂ = k₂c₂ (4)

Суммарная скорость образования Р

w = w₁ + w₂

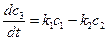(5)

Подставим с₁ из (3) в (5)

(6)

После ряда математических преобразований получим выражение для с₃:

(7)

Теперь найдем с₂:

т.к. (8)

то после математических преобразований получим:

(9)

k₁ k₂

2 случай. A→P↔B (1)

k_-2

Считаем, что 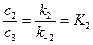(2)

с₁ = с₁₀е^-k1t (3)

(4)

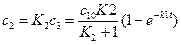(5)

k₁ k₂

3 случай. A↔P→B (1)

k_-1

Считаем, что (2)

с₁ = с₁₀е^-k2t (3)

(4)

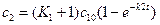(5)

4. Сопряженные реакции

По Шилову Н.А. – когда самопроизвольно идущая в системе реакция вызывает протекание другой реакции, не осуществимой в отсутствии первой – химическая индукция.

Две реакции, одна из которых индуцирует протекание другой, называются сопряженными.

Пример: А + В → М

A + B + C → M + N (1)

А + С → N

Вещество В вызывает реакцию А и С. Вещество А – актор, В – индуктор, С – акцептор.

Фактор индукции Ф – количественная характеристика эффективности химической индукции – отношение скорости расходования акцептора на скорость расходования индуктора.

5. Автокаталитические реакции.

Реакция называется автокаталитической, если она ускоряется одним из продуктов реакции.

Рассмотрим автокаталитическую реакцию, идущую в две стадии.

k₁

А + В → D – лимитирующая стадия

D → 2В – быстрая стадия (1)

А → В – суммарная реакция

где А – исходное вещество

D – промежуточное состояние

B – продукт – катализатор

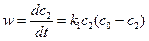(2)

с₂ – концентрация В в момент t

с₁ = с₀ – с₂ – концентрация А в момент t

с₀ = с₁₀ + с₂₀ = с₁ + с₂ (3)

где с₀ – сумма начальных концентраций веществ А и В.

w

c_2max c₂

c₂

c₀

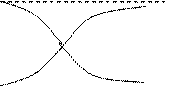t_1/2 t

w

w_max

t_max t

Рис. Зависимости от времени: 1 – скорости автокаталитической реакции; 2 – концентрации исходного вещества; 3 -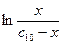

Дата добавления: 2015-08-10