Індивідуальні завдання за темою

«Регресійний аналіз оцінювання зв’язку між економічними показниками»

1 За даними таблиці 3 побудувати матрицю парних коефіцієнтів кореляції. В якості залежної змінної взяти перший показник з таблиці, тобто «Виручка від реалізації продукції». П’ять-шість інших показників з таблиці – за обґрунтованим вибором – використовуються як незалежні змінні.

2 Із незалежних показників обрати два, які мають більш тісний кореляційний зв’язок з залежною змінною, та оцінити параметри моделі залежності виручки від реалізації від двох обраних факторів (незалежних змінних).

3 Виконати аналіз побудованої моделі і дати висновки.

4 Якщо побудована модель є адекватною, зробити прогноз з її використанням.

Таблиця 13 – Варіанти завдань

Варіант	Номери показників, що використовуються як незалежні змінні
	2, 7, 8, 11, 14
	14, 17, 18, 20, 21, 10
	8, 7, 10,12, 13,20
	3, 13,17, 18, 20
	20, 7,10, 11, 19
	21, 9, 17, 19, 4
	17, 13, 5, 12, 11
	14, 7, 4, 20, 18
	17, 18, 19, 13, 14
	3, 13, 15, 17, 18, 19

Методичні вказівки до виконання завдань

Питання регресійного аналізу та оцінки параметрів економетричних моделей докладно викладено в навчальній літературі [10], [12], [13], [14], та [1], [2], [3], [4].

При визначенні конкретних залежностей одні показники розглядаються як фактори впливу (ознаки), що обумовлюють зміну іншого показника (результативний показник). Функціональні взаємозв’язки характеризуються повною відповідністю між змінами факторної ознаки і змінами результативної величини, причому кожному значенню фактора-ознаки відповідає певне значення результативного показника. При кореляційних зв’язках між змінами факторів-ознак та результативного показника повної відповідності не існує. Вплив окремих факторів виявляється лише в середньому при значній кількості спостережень фактичних даних. Крім того фактор-ознака, як правило, залежить від зміни інших показників.

Форма взаємозв’язку випадкових величин і їх функції дістали назву рівняння регресії. Виділяють парну (просту) та множинну регресії лінійного та нелінійного (квадратичного, експоненційного, напівлогарифмічного) типів. Вид, а також параметри рівняння регресії, знаходять за допомогою методу найменших квадратів. За наявності кореляційної залежності визначають лише тенденцію зміни результативного показника при змінах факторів-ознак.

Найчастіше застосовуються такі математичні залежності для оцінювання кореляційного зв’язку між факторами:

- прямолінійна:

y = a₀ + a₁x,

де а₀ – стала (область існування моделі);

а₁ – коефіцієнт регресії, що характеризує середню зміну результативного показника при змінах фактора-ознаки;

- параболічна:

y = a₀ + a₁x + a₂x² ;

- показникова:

y = a₀ · a₁^x ;

- степенева:

y = a₀ + x^a₁;

- гіперболічна:

y = a₀ + a₁/x;

- напівлогарифмічна:

y = a₀ + a₁·lg x.

Статистичне оцінювання тісноти зв’язку між залежною і незалежними змінними ґрунтується на показниках варіації:

- загальній дисперсії 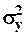результативного показника, обумовленій впливом усіх факторів у сукупності;

- факторній дисперсії результативного показника, що показує його варіацію під впливом окремих факторів;

- залишковій дисперсії результативного показника, яка показує його варіацію під впливом усіх факторів, крім виділених, причому

; ; ;

= + .

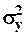Якісною оцінкою ступеня зв’язку випадкової величини виступають:

- коефіцієнт детермінації, який визначається відношенням факторної та загальної дисперсій: R² = / 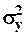. Значення показника змінюється в межах від 0 до +1. Якщо коефіцієнт детермінації R² > 0,7, то варіація залежної змінної в основному обумовлена впливом обраних факторів і побудовані регресійні моделі можна використовувати для прогнозування;

- індекс кореляції, який розраховується як квадратний корінь із коефіцієнта детермінації, тобто , причому його значення лежать у межах від –1 до +1. Знак «+» вказує на наявність прямого зв’язку, «–» – зворотного.

Для оцінки значущості індексу кореляції можна використовувати F-критерій Фішера:

,

де n – число значень у масиві;

m – число параметрів рівняння регресії (факторів).

Фактичне значення цього критерію порівнюють із критичним значенням, яке визначають з урахуванням рівня значущості та кількості ступенів вільності. Якщо фактичне значення F-крітерію Фішера більше від критичного, то індекс кореляції вважається істотним.

Якщо аналізується невелика сукупність даних (n < 30), то для оцінювання значущості індексу кореляції використовується t-критерій Ст’юдента, який розраховується таким чином:

.

Розраховане значення t-критерію для індексу кореляції порівнюється з критичним з урахуванням прийнятого рівня значущості, а також кількості ступенів вільності та індекс кореляції R вважається значущім, якщо t_p > t_k. Аналогічно оцінюється значущість оцінки параметрів моделі на основі t-критерію для параметрів моделі:

; .

Табличний процесор дає змогу використати різні інструменти «Пакета аналізу» для одержання параметрів лінійної парної та множинної регресій, а також оцінки ступеня зв’язку.

Для оцінювання парного кореляційного зв’язку між показниками можна використати також статистичну функцію КОРРЕЛ. Для цього поетапно розраховують кожну пару коефіцієнтів і будують матрицю парних коефіцієнтів кореляції.

Лінійний регресійний аналіз полягає у виборі графіка для відображення спостережень за допомогою методу найменших квадратів. Регресія використовується для аналізу впливу на залежну змінну значень однієї або більше незалежних змінних-факторів. Одержане рівняння залежності можна використовувати для прогнозних розрахунків: підставляючи у рівняння нові значення х_j можна отримати прогнозне значення у.

Для розширеного аналізу можна також розрахувати такий показник, як коефіцієнт еластичності:

,

де a_j – коефіцієнт у рівнянні залежності для j-того фактора;

– середньоарифметичне значення j-того фактора;

– середньоарифметичне значення результативного показника.

Коефіцієнт еластичності показує, на скільки відсотків у середньому змінюється результативний показник із зміною аргументу x_j на 1%.

При проведенні кореляційно-регресійного аналізу можна застосовувати такі статистичні функції для оцінювання параметрів моделі та залежності між факторами: ЛИНЕЙН, КВПИРСОН, КОВАР, КОРРЕЛ, FРАСП.

Приклади завдань для самостійної роботи за темою

«Регресійний аналіз оцінювання зв’язку між економічними показниками»

Завдання 1.

У таблиці 14 наведено дані про кількість телефонів на 1000 осіб (у) та валовий внутрішній продукт (ВНП) на душу населення (х) в західному регіоні України (дані умовні) в 1976-1997 рр.

Таблиця 14 – Кількість телефонів та ВНП на душу населення

в західному регіоні України, 1976-1997 рр.

Рік	у	х	Рік	у	х
		1 299			2 462
	36,5				2 723
		1 365			3 033
		1 409			3 317
		1 549			3 487
		1 416			3 575
		1 473			3 784
		1 589			4 025
		1 757			4 286
		1 947			4 628
		2 204			5 038

1. Використовуючи дані таблиці 14, побудувати лінійну регресійну модель.

2. Розрахувати невідомі параметри, перевірити параметри на значущість, побудувати інтервали довіри для параметрів.

3. Проінтерпретувати таблицю АNOVA-дисперсійного аналізу.

4. Розрахувати прогноз кількості телефонів на 1998 рік.

5. Побудувати інтервали довіри для прогнозу.

Завдання 2.

У таблиці 15 наведено дані про ціни на золото, індекс споживчих цін (CPI) та індекс Нью-Йоркскої фондової біржі (NYSE) в Сполучених Штатах за період 1977-1991 рр. Індекс NYSE включає більшість акцій, зареєстрованих на NYSE, приблизно понад 1500.

Таблиця 15

Рік	Ціна на золото в Нью-Йорку, $ за тройську унцію	Індекс споживчих цін (CPI), 1982-84=100	Індекс Нью-Йоркської фондової біржі (NYSE), 31.12.1965=100
	147,98	60,6	53,69
	193,44	65,2	53,70
	307,62	72,6	58,32
	612,51	82,4	68,10
	459,61	90,9	74,02
	376,01	96,5	68,93
	423,83	99,6	92,63
	360,29	103,9	92,46
	317,30	107,6	108,90

Продовження таблиці 15

	367,87	109,6	136,00
	446,50	113,6	161,70
	436,93	118,3	149,91
	381,28	124,0	180,02
	384,08	130,7	183,46
	362,04	136,2	206,33

Інвестування вважається страховкою від інфляції, якщо ставка процента вища за рівень інфляції або знаходиться на тому ж рівні. Щоб перевірити цю гіпотезу вважайте, що підходять такі моделі:

Gold price_t = b₀ + b₁CPI_t + e_t,

NYSE Index_t = b₀ + b₁CPI_t + e_t.

Розрахуйте параметри цих моделей.

Яке страхування від інфляції краще: золото чи фондова біржа?

Дата добавления: 2015-07-25