Размерность и базис векторного пространства

n – мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде , где 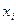– i -я компонента вектора x.

Векторным пространством называется множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее свойствам (аксиомам) линейных операций над векторами:

1) – коммутативное (переместительное) свойство;

2) – ассоциативное (сочетательное) свойство суммы;

3) 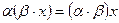– ассоциативное относительно числового множителя свойство;

4) – дистрибутивное (распределительное) относительно суммы векторов свойство;

5) – дистрибутивное относительно суммы числовых множителей свойство;

6) существует нулевой вектор такой, что для любого вектора ;

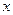7) для любого вектора 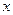существует противоположный вектор такой, что ;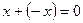

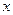8) для любого вектора (особая роль числового множителя 1).

Вектор называется линейной комбинацией векторов векторного пространства , если он равен сумме произведений этих векторов на некоторые действительные числа:

где 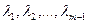– некоторые действительные числа.

Векторы 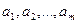векторного пространства называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что выполняется равенство:

В противном случае векторы 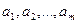называются линейно независимыми.

Пример 4.1. Являются ли векторы линейно зависимыми?

Решение. Составим векторное равенство:

Запишем в виде вектор-столбцов:

Таким образом, задача свелась к решению системы уравнений:

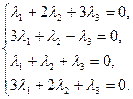
Преобразуем систему методом Гаусса:

~ ~ ~ .

Если то где C – произвольное число.

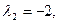
Пусть C =1, тогда: следовательно, эти векторы – линейно зависимые.

Векторное пространство 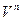называется n -мерным, если в нем существуют n линейно независимых векторов, а любые из (n +1) векторов уже являются зависимыми.

Рассмотренное нами линейное векторное пространство очевидно n -мерно.

Совокупность n линейно независимых векторов n -мерного пространства называется базисом.

Теорема. Каждый вектор 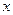линейного пространства можно представить и притом единственным способом в виде линейной комбинации векторов базиса (доказательство опустим).

Итак, равенство:

где 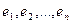– векторы базиса n -мерного пространства R, – не равные одновременно нулю числа, называется разложением вектора x по базису 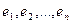, а числа – координатами вектора x относительно этого базиса.

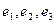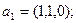
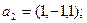
Пример 4.2. В базисе заданы векторы 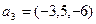. Показать, что векторы 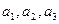образуют базис.

Решение. Векторы 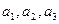должны быть линейно независимыми. Составим векторное равенство:

Решим систему уравнений:

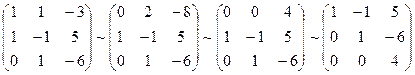, следовательно, 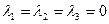– единственное нулевое решение.

Таким образом, векторы 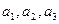образуют систему линейно независимых векторов и, следовательно, составляют базис.

Дата добавления: 2015-07-25