Читайте также:
|
В пространстве имеются два базиса: старый –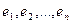 
и новый – 
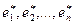. Векторы нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
Переход от старого базиса к новому задается матрицей перехода:
.
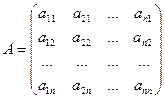Коэффициенты разложения новых базисных векторов по старому базису образуют столбцы матрицы. Матрица A – неособенная. Обратный переход от нового базиса к старому осуществляется с помощью обратной матрицы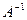 
.
Зависимость между координатами вектора x относительно старого и нового базисов:
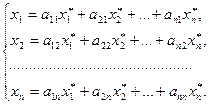
В матричной форме:
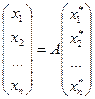или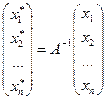 
.
Пример 4.3. Выяснить, образуют ли векторы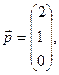 
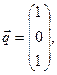
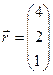базис. Если образуют, то разложить вектор 
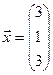по этому базису.
Решение. Векторы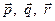 
должны быть линейно независимыми. Составим векторное равенство:
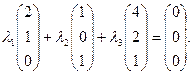Запишем в виде системы уравнений: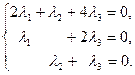 
Преобразуем систему методом Гаусса: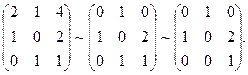 
Следовательно, 
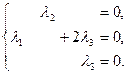таким образом, 
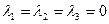, это значит, что векторы 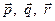линейно независимы и образуют базис.
Разложим вектор 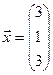по данному базису. Матрица перехода имеет вид:
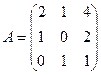; D(A) = –1; 
; 
.
.
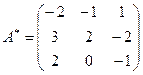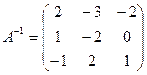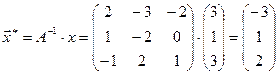Таким образом,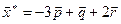 
.
Пример 4.4. Вектор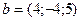 
, заданный в базисе 
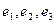, выразить в базисе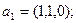 
.
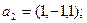
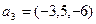Решение. Связь между базисами:
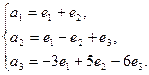
Матрица перехода от базиса 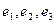к базису 
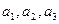имеет вид: 
.
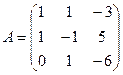Вычислим обратную матрицу: D(A) =4;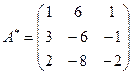 
; 
.
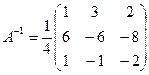Таким образом,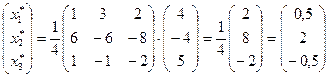 
.
Новые координаты вектора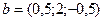 
в базисе 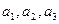. Вектор b может быть представлен в виде: 
.
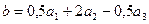Задания для самостоятельного решения:
Дата добавления: 2015-07-25; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Размерность и базис векторного пространства | | | Когда придут на тебя все слова сии - благословение и проклятие, которые изложил я тебе, и примешь [их] к сердцу своему среди всех народов, в которых рассеет тебя Господь Бог твой. |