Теория газовой хроматографии

Важным этапом в развитии теории газовой хроматографии была опубликованная в 1956 г. работа Ван-Димтера, Цвидервега и Клинкенберга, посвященная вопросам развития хроматографической зоны. На основе изучения влияния диффузионных и кине­тических факторов они вывели ставшее классическим уравнение, получившее название уравнения Ван-Димтера. Если длину ко­лонки разделить на число теоретических тарелок, то получаемая величина Н = L/п — высота, эквивалентная теоретической та­релке, представляет собой высоту цилиндрика с сорбентом, на котором достигается равновесие между газовой и сорбирующей фазами. Концентрация сорбата в газовом потоке, покидающем этот участок колонки, является равновесной по отношению к средней концентрации сорбата в растворе неподвижной фазы (или в адсорбированном состоянии), т. е. отношение концентра­ций равно коэффициенту распределения Г. Чем меньше величина H, тем больше ступеней равновесия (теоретических тарелок) до­стигается в колонке. Соотношение, полученное Ван-Димтером и его соавторами, представляет собой зависимость между высо­той, эквивалентной теоретической тарелке, и скоростью газа-но­сителя а:

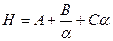
Каков физический смысл этого уравнения? Вполне понятно, что уменьшение скорости газа-носителя соответствует увеличе­нию времени пребывания молекул сорбата в колонке. Следова­тельно, слагаемое В/а описывает влияние продольной диффузии молекул, величина В пропорциональна коэффициенту диффузии сорбата в газовой среде. Последнее слагаемое Са описывает про­цесс внутренней диффузии, т.е. движение молекул сорбата в пленке неподвижной жид­кости или в порах адсорбента. Чем меньше толщина пленки и чем больше коэффициент диффузии сорбата в жид­кости, тем меньше значение С и тем быстрее молекулы возвратятся в газовую фазу. Роль этого фактора становит­ся значительной при высоких скоростях газа. Слагаемое А характеризует влияние так -

называемой вихревой диффузии, т. е. завихрения потока вокруг частиц сорбента. В первом приближении это слагаемое не за­висит от скорости газа-носителя.

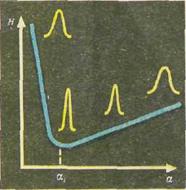
Анализ уравнения Ван-Димтера показывает, что при увеличе­нии скорости газа, а уменьшается второй член уравнения В/а и увеличивается третий член Са, причем изменение Са постепен­но опережает изменения В/а так, что значение Н сначала быстро падает, а затем после прохождения скоростью некоторого значе­ния а₁, начинает снова медленно возрастать. Таким образом, значение а, при котором Н наименьшее, будет оптимальным, ведь наименьшее Н соответствует максимальной эффективности колонки.

Работа Ван-Димтера, а также последующие исследования Джонса, Жуховицкого и Гиддингса стали теоретической базой, на основе которой разрабатывались и разрабатываются способы выбора наилучших условий хроматографического разделения ве­ществ: скорости газа-носителя (обычно вблизи минимума Я), ко­личества неподвижной фазы, размера зерен твердого носителя или адсорбента и т.д. Это и позволило достичь эффективности колонок в тысячи теоретических тарелок.

Однако если такая эффективность была достаточной, чтобы разделить, например, все изомерные гексаны и гептаны, то для детального анализа октанов, а тем более нонанов было необхо­димо еще резко увеличить разделяющую способность. И в 1957 г. М. Ролей предложил вместо насадочных колонок рабо­тать с длинными капиллярами.

Дата добавления: 2015-07-21