
|
Читайте также: |
По дисциплине: «Лесосплавной флот»
На тему: «Расчет элементов плавучести и остойчивости судов и плавучих оснований»
Выполнила: студента ЛИ2-092-ОС
Зоиров Б.Ш.
Проверил: проф. Мануковский А.Ю.
Воронеж 2013
Введение
Разнообразие и спецификация природно-производственных условий на водном транспорте леса предопределили необходимость создания специализированного лесосплавного флота, в состав которого входят транспортные, технические, вспомогательные, служебно – разъездные Ии некоторые другие судна. Лесосплавной флот является одним из основных видов технического оснащения лесосплавных предприятий, применение которого в производственном процессе водного лесотранспорта позволяет осуществлять комплексную механизацию основных и вспомогательных работ, повысить производительность труда, снизить стоимость лесопродукции и ускорить доставку лесоматериалов потребителям. Проектирование, строительство и эксплуатация лесосплавных судов основаны на «теории корабля», которая применима для всех судов и кораблей.
Целью работы является закрепление теоретического материала по дисциплине, овладение методами расчета элементов плавучести и остойчивости судов и плавучих оснований лесосплавных машин.
В работе проводятся общие сведении о проектируемом судне (главные размерения, коэффициент полноты, объем водоизмещения, метацентрические высота и радиус), полученные в результате выполнения РГР.
Построение теоретического чертежа корпуса судна
Построение теоретического чертежа корпуса судна необходимо для
дальнейших расчетов, с него будут сниматься величины размерных характеристик.
Корпус судна представляет собой сложную криволинейную поверхность,
которая рассматривается относительно трех взаимно перпендикулярных главных плоскостей: диаметральной (ДП), основной (ОП), плоскостью мидельшпангоута О.
Горизонтальная продольная плоскость, параллельная ОП, совпадающая с
поверхностью спокойной воды при расчетной осадке судна, называется плоскостью конструктивной ватерлинии (КВЛ).
Подробнее изложено в литературе [1, 2].
Линии ДП, ОП и О образуют судовые координатные оси: ось абсцисс
ОХ - линия пересечения ДП и ОП:, ось ординат ОУ - линия пересечения ОП и О ось аппликат - линия пересечения ДП и О.
Главные плоскости сечения корпуса судна изображены на рис.1.
Для изображения поверхности корпуса вычерчивают его теоретический
чертеж, состоящий из трех проекций: ≪бока≫, на котором показаны проекции обводов корпуса судна на ДП: ≪полушироты≫, на которой изображены проекции обводов корпуса судна на плоскость КВЛ: ≪корпуса≫, на котором даны проекции обводов корпуса судна на плоскость О [1, 2].
Для построения теоретического чертежа корпус судна мысленно рассекают рядом плоскостей, проведенных параллельно главным плоскостям. Проекции
линий пересечения судовой поверхности с секущими плоскостями и составляют теоретический чертеж судна.
Линии пересечения корпуса судна с плоскостями, параллельными ДП, на-
зываются батоксами. На ≪боку≫ батоксы изображаются в своем истинном виде, на ≪полушироте≫- в виде горизонтальных прямых линий, на ≪корпусе≫- в виде вертикальных прямых линий.
Линии пересечения корпуса судна с плоскостями, параллельными плос-
кости ОП или КВЛ, называются ватерлиниями. На ≪полушироте≫ ватерлинии изображаются в своем истинном виде, на ≪боку≫ и ≪корпусе≫- в виде горизонтальных прямых линий. Так как корпус судна симметричен относительно ДП, ватерлинии вычерчивают только на один борт от ДП.
Линии пересечения корпуса судна с плоскостями, параллельными плос-
кости О, называются шпангоутами. На ≪корпусе≫ шпангоуты изображаются в своем истинном виде, а на ≪боку≫ и ≪полушироте≫ - в виде вертикальных прямых линий. Так как корпус судна симметричен относительно ДП, каждый из шпангоутов вычерчивают только на один борт: при этом справа от ДП обычно изображают носовые, а слева - кормовые шпангоуты.
Для практической работы число секущих плоскостей (шпангоутов и ва-
терлиний) задано. Количество их определяется по выданной в задании проек-
ции ≪корпуса≫, где они изображены и пронумерованы. По ≪корпусу≫ с учетом заданного масштаба определяются и расстояния, через которые проведены секущие плоскости.
Расстояние (_Т) между соседними ватерлиниями снимается измерителем
с чертежа проекции ≪ корпус≫ и по масштабу изображения переводится в метры.
Расстояние (_L) между соседними шпангоутами определяется либо как
отношение заданной длины судна L в метрах к числу шпангоутов, подсчитанных по заданной проекции, либо оно задано.
Далее в методических указаниях в формах таблиц и на рисунках рас-
смотрен пример для подводной части корпуса, поделенного четырьмя ватерлиниями и двадцатью шпангоутами. Количество секущих плоскостей ватерлиний и шпангоутов может быть различным, и заданно на проекции ≪корпус≫. Числовые примеры основных расчётов рассмотрены в литературе [1, 2].
Построение теоретического чертежа начинается с вычерчивания его сетки, которая представляет собой совокупность горизонтальных и вертикальных
прямых линий, являющихся следами батоксов, ватерлиний и шпангоутов. Сетка вычерчивается по заданным в работе главным размерениям судна(расчетной длины L, расчётной ширины B, высоты и расчётной осадки Т) и определённым выше числом секущих плоскостей в удобном рекомендуемом масштабе (см.ниже).
Построение сетки ведут в следующем порядке:
1 Размечают места расположения проекций так, чтобы ≪полуширота≫ на-
ходилась точно под ≪ боком≫, а ≪корпус≫- точно на уровне ≪бока≫, и при этом расстояние между проекциями было достаточным.
2 Под линейку, выверенную на прямолинейность, проводят основную ли-
нию на ≪боку≫ и ≪корпусе≫ и след ДП- на ≪полушироте≫.
3 На проведенных линиях откладывают: на ≪боку≫ и ≪полушироте≫ - длину судна между перпендикулярами L⊥⊥, а на ≪корпусе≫ - ширину судна B.
4 Длину судна на ≪боку≫ и ≪полушироте≫ с максимальной точностью де-
лят на равные части _L- по числу промежутков между шпациями, а ши-
рину судна на ≪корпусе≫ - по числу промежутков между батоксами. В
точках деления методом засечек восстанавливают перпендикуляры.
5 На этих перпендикулярах откладывают: на ≪боку≫ и ≪корпусе≫ – высоту борта H, среднюю осадку T и расстояние между ватерлиниями _T, а на ≪полушироте≫ - половину ширины судна и расстояния между батокса-ми. Одноименные точки соединяют прямыми.
По мере проведения прямых образуются прямоугольники. Поэтому для
контроля правильности построений проверяют равенство диагоналей всех равновеликих прямоугольников. Видимого расхождения в диагоналях быть не должно.
Поскольку шпангоуты, ватерлинии и батоксы изображают одну и ту же
судовую поверхность, они должны быть согласованы на всех проекциях теоретического чертежа. На этом основано построение ватерлиний на ≪полушироте≫ и батоксов на ≪боке≫.
При согласовании точки пересечения каждого шпангоута со всеми ватер-
линиями и батоксами переносятся с заданной проекции ≪корпус≫ на ≪полушироту≫ и на ≪бок≫. Ватерлинии и шпангоуты согласуют между собой по ширине (ордината y), ватерлинии и батоксы - по длине (абсцисса x), а батоксы и шпангоуты - по высоте (апликата z) судна.
2 Вычисление объемного водоизмещения
Объем воды V, вытесняемой подводной частью судна, называется объемным водоизмещением.
V= 2∆L∆T∑∑, м3; (2.1)
Где ∆L- расстояние между шпангоутами – теоретическая шпация;
∆T – расстояние между погруженными ватерлиниями.
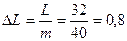 м (2.2)
м (2.2)
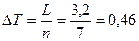 м (2.3)
м (2.3)
V=2∙0,8∙0,46∙34150=25134,4 м3
Исходные данные:
L= 32 м;
T= 3,2 м;
B= 9,0 м;
Р= 1,9 т.
3 Определение коэффициентов полноты корпуса судна
Объемное водоизмещение, площади КВЛ и О судна могут быть определены без специальных расчетов, если известны коэффициенты полноты корпуса судна безразмерные коэффициенты, позволяющие судить о форме обводов
корпуса судна.
Коэффициент полноты площади конструктивной ватерлинии КВЛ S к
площади описанного прямоугольника со сторонами, равными длине судна L и его ширине В, подсчитывается по формуле
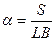 (3.1)
(3.1)
Где L- длина судна(L= 32 м); В- ширина судна (В=9 м)
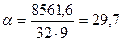
Коэффициент полноты площади мидель-шпангоута β, равный отношению погруженной площади мидель-шпангоута ω0 к площади описанного прямоугольника со сторонами, равными ширине судна В и его осадке Т, подсчитывается но формуле
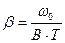 (3.2)
(3.2)
Где Т- осадка судна (Т=3,2 м)
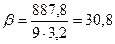
Коэффициент полноты водоизмещения δ, равный отношению объема V
подводной части судна к V’ параллелепипеда, построенного на главных размерах – длине L, ширине B, осадке Т, подсчитывается по формуле
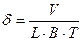 (3.3)
(3.3)
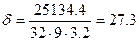
Коэффициент продольной полноты ϕ, равный отношению объемного водоизмещения V к объему цилиндра с основанием, равным погруженной площади мидель-шпангоута ωO, и высотой, равной длине судна L, определяется по формуле
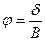 (3.4)
(3.4)
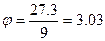
Коэффициент вертикальной полноты ψ, равный отношению объемного
водоизмещения V к объему цилиндра с основанием, равным площади КВЛ S и высотой, равной осадке Т, вычисляется по формуле:
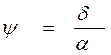
(3.5)
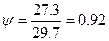
По этим коэффициентам судят о мореходных и эксплуатационных качествах
судов (остойчивость, грузовместимость, грузоподъемность, сопротивление воды движущегося судна) изложенных [1,2].
4 Определение координат центра тяжести площади конструктивной
ватерлинии
Для расчетов остойчивости необходимо знать положение координаты
(абсциссу и ординату) центра тяжести площади КВЛ.
Ввиду симметричности площади КВЛ относительно оси Х ордината центра тяжести Уf = 0.
Абсциссу центра тяжести площади КВЛ и абсциссы Xf определяют как
частное от деления статического момента Му этой площади относительно оси Y на площадь КВЛ, по формуле
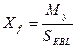 (4.1)
(4.1)
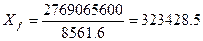
Вычисление статического момента площади КВЛ и абсциссы Xf центра
тяжести ее выполняют по данным теоретического чертежа (проекция ≪корпус≫,ординаты Уi для КВЛ) или при вычислении объемного водоизмещения в расчетной табл.1 (значения ординат Уi для КВЛ, для примера табл.1 это от У40 до
У420).
Расчеты удобно свести в форму табл.2.
Таблица 2
Вычисление абсциссы центра тяжести площади КВЛ
| Номер шпангоута | Коэффициенты при ординатах Ki | Ординаты КВЛ Yi, м | Произведение Ki Yi, м |
| -1 | -150 | ||
| -2 | -300 | ||
| -3 | -450 | ||
| -4 | -600 | ||
| -5 | -750 | ||
| -6 | -900 | ||
| -7 | -1050 | ||
| -8 | -1200 | ||
| -9 | -1350 | ||
| -10 | -1500 | ||
| -11 | -1650 | ||
| -12 | -1800 | ||
| -13 | -1950 | ||
| -14 | -1260 | ||
| -15 | -1350 | ||
| -16 | -1440 | ||
| -17 | -1530 | ||
| -18 | -1620 | ||
| -19 | -1720 | ||
| -20 | -1800 | ||
| Сумма | ∑Yi | ||
| Поправка | П= 1/20(Y1+Y40) | 6,8 | |
| Исправленная сумма | Sиспр=∑Yi-1/20(Y1+Y40) | 401,2 | |
| S | Xв=Sиспр/SКВL | 0,046 |
5 Определение координат центра величины
Центром величины называется центр тяжести объема водоизмещения
судна. Таким образом, вычисление координат центра величины сводится к определению положения центра тяжести подводного объема корпуса судна относительно его координатных осей.
Ввиду симметрии корпуса судна относительно ДП ордината центра вели-
чины: Уc =0.
Абсцисса центра величины Xc определяется как отношение статического
момента подводного объема корпуса Мyz относительно плоскости YOZ к объемному водоизмещению V, вычисляется по формуле:
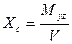 (5.1)
(5.1)
Аппликата центра величины Zc определяется как отношение статическо-
го момента подводного объема корпуса Мух относительно плоскости УОХ к
объемному водоизмещению V, подсчитывается по формуле
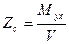 (5.2)
(5.2)
5.1 Вычисление абсциссы центра величины
Таблица 3
Вычисление абсциссы центра тяжести
| Номера шпангоутов | Площади шпангоутов | Множители плеч | Произведение разности площадей шпангоутов и множителей плеч | |||||
| носовых | кормовых | носовых | кормовых | |||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 887,8 | 887,8 | |||||||
| 884,12 | 887,8 | -40,48 | ||||||
| 873,54 | 882,28 | -104,88 | ||||||
| 837,2 | 891,48 | -705,64 | ||||||
| 770,04 | 538,2 | 3245,76 | ||||||
| 686,78 | 538,2 | 2228,7 | ||||||
| 570,4 | 538,2 | 515,2 |
Продолжение табл. 4
| 376,28 | 538,2 | -2752,64 | |||||||
| 172,04 | 538,2 | -6590,88 | |||||||
| 77,74 | 538,2 | -8748,74 | |||||||
| 21,16 | 538,2 | -10340,8 | |||||||
| Сумма ∑m∆ω | -23294,4 | ||||||||
| Поправка П=1/10(ω0- ω40) | -5170,4 | ||||||||
| Исправленная сумма Sиспр= ∑m∆ω-1/10(ω0- ω40) | -18124 | ||||||||
| Абсцисса центра величины | 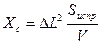
| -0,45 | |||||||
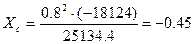
5.2 Вычисление аппликаты центра величины
Таблица 4
Вычисление аппликаты центра величины
| Площадь ватерлиний | Множители плеч | Произведение площадей ватерлиний на множители плеч |
| S0=0 | ||
| S1=7344 | ||
| S2=7841,6 | 15683,2 | |
| S3=8019,2 | 24057,6 | |
| S4=8097,6 | 32390,4 | |
| S5=8187,2 | ||
| S6=8464 | ||
| S7=8561,6 | 59931,2 | |
| Сумма | ∑mSi | 231126,4 |
| Поправка | П=7/2S7 | 209759,2 |
| Исправленная сумма | Sиспр=∑mSi - 7/2S7 | 21367,2 |
| Аппликата центра величины, м | 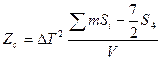
| 0,19 |
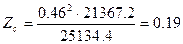
6 Кривая водоизмещения - грузовой размер
В процессе эксплуатации судов и плавучих лесосплавных механизмов
изменяется их загрузка (прием и расходование грузов), а также при ремонте и
модернизации судов часто приходится иметь дело с изменением их водоизмещения, а следовательно, и осадки. Зависимость изменения водоизмещения от осадки показывает кривая водоизмещения на рис.6.
Для построения кривой водоизмещения используют строевую по ватер-
линиям. Согласно свойству строевой по ватерлиниям площадь, ограниченная
строевой, осями координат и рассматриваемой ватерлинией, выражает объемное водоизмещение при погружении корпуса по данную ватерлинию.
Так как объемное определяется интегралом вида
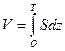 (6.1)
(6.1)
то, следовательно, уравнение кривой водоизмещения может быть представлено в виде интеграла с переменным верхним пределом
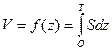 (6.2)
(6.2)
где S = f(z) - переменная по углублению Z площадь ватерлинии.
Из этого следует, что график функции V=f(z) представляет собой интеграль-
ную кривую к графику функции S= f(z), называемому строевой по ватерлиниям. Следовательно, кривая водоизмещения есть интегральная кривая по отношению к строевой по ватерлиниям. Ординаты кривой водоизмещения вычисляются как частные значения интеграла с переменным верхним пределом. Основная кривая (строевая по ватерлиниям) задается графически, поэтому численные значения ординат интегральной кривой, представляющие собой в масштабе часть площади строевой по ватерлиниям, могут быть определены по
правилу трапеций [1, 2], а именно:
- водоизмещение по 1-ю ватерлинию составит
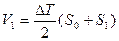 (6.3)
(6.3)
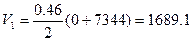 м3
м3
- водоизмещение по 2-ю ватерлинию
 (6.4)
(6.4)
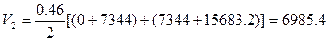 м3
м3
- водоизмещение по 3-ю ватерлинию
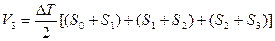 (6.5)
(6.5)
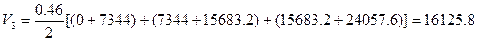 м3
м3
- водоизмещение по 4-ю ватерлинию
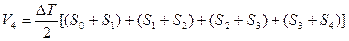 (6.6)
(6.6)
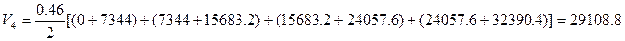
- водоизмещение по 5-ю ватерлинию
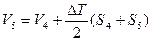 (6.7)
(6.7)
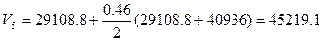
- водоизмещение по 6-ю ватерлинию
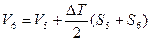 (6.8)
(6.8)
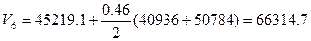
- водоизмещение по 7-ю ватерлинию
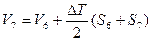 (6.9)
(6.9)
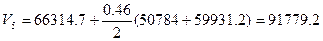
где ∆Т - расстояние между соседними ватерлиниями, м;
S0, S1, S2, S3, S4 - площади ватерлиний, м2.
Площади Si соответствующих ватерлиний берутся из табл.1, а c Т - по
теоретическому чертежу.
Грузоподъемностью, или дедвейтом судна называется масса грузов, которую может принять судно, будучи в порожнем состоянии, до погружения на допустимую осадку.
Используя кривую водоизмещения, требуется определить грузоподъемность судна при
T0=0.3T (6.10)
Т0=0,3*3,2=0,96
где Т - осадка судна по КВЛ, м, берется с теоретического чертежа.
7 Вычисление элементов начальной остойчивости судна
Остойчивостью называется способность судна, выведенного из положения равновесия внешними силами и предоставленного самому себе, вновь возвращаться в первоначальное положение равновесия после того, как действие внешних сил прекратилось.
Наклонение судна в поперечной плоскости называется креном, в про-
дольной плоскости - дифферентом.
Главнейшим положением метода начальной остойчивости является тео-
рема Эйлера о равнообъемных наклонениях.
7.1 Вычисление моментов инерции площади ватерлинии
Предварительные расчеты для определения моментов инерции удобно
свести в форму табл.5.
Таблица 5
Вычисление моментов инерции площади ватерлинии
| Номер шпангоута | Множи-тели плеч | Квадраты Множителей i | Ординаты КВЛ | Кубы ординат | Произве-дение |
| -1 | |||||
| -2 | |||||
| -3 |
Продолжение табл. 5
| -4 | |||||
| -5 | |||||
| -6 | |||||
| -7 | |||||
| -8 | |||||
| -9 | |||||
| -10 | |||||
| -11 | |||||
| -12 | |||||
| -13 | |||||
| -14 | |||||
| -15 | |||||
| -16 | |||||
| -17 | |||||
| -18 | |||||
| -19 | |||||
| -20 | |||||
| Сумма | |||||
| Поправка | |||||
| Исправленная сумма |
По предварительным расчетам вычисляются моменты инерции по формулам
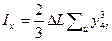 (7.1)
(7.1)
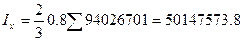
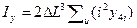 (7.2)
(7.2)
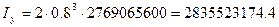
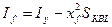 (7.3)
(7.3)
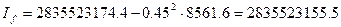
где cL - расстояние между шпациями, м2;
Sквл - площадь КВЛ, м,
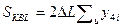 ; (7.4)
; (7.4)
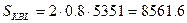
х - абсцисса центра тяжести КВЛ, м, пункт 5.
7.2 Вычисление метацентрических радиусов
Поперечный метацентрический радиус Р равняется моменту инерции Ix площади действующей ватерлинии относительно ее центральной продольной оси, деленному на объемное водоизмещение судна по V по действующую ватерлинию, подсчитывается по формуле
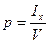 (7.5)
(7.5)
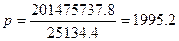 м
м
При дифференте равнообъемное наклонение происходит вокруг попе-
речной оси, проходящей через центр тяжести действующей ватерлинии. Про-
дольный метацентрический радиус вычисляется по формуле
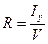 (7.6)
(7.6)
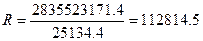 м
м
где Iy – момент инерции площади действующей ватерлинии относитель-
но поперечной оси, м4;
V – объемное водоизмещение по действующую ватерлинию, м3.
7.3 Вычисление метацентрических высот
h=ρ+zc-zG; (7.7)
h=1995.2+0.19-0.28=1995.11
H=R+zc-zG; (7.8)
H=112814.5+0.19-0.28=112814.41
где Р и R - соответственно поперечный и продольный метацентрические
радиусы, м;
Z с - апликата центра величины, м, пункт 6;
ZG - апликата центра тяжести, м, принимается равной ZG = 1,5 Zc.
7.3Изменение остойчивости судна при приеме груза
При приеме груза изменяются осадка и водоизмещение судна, положение
центра тяжести, центра величины и метацентра, а в связи с этим
изменяется поперечная и продольная метацентрические высоты.
В работе для заданного корпуса рассчитывают изменение этих
величин, помещая на судно груз с заданным весом р.
Для этого положения груза вычисляются новые величины элементов ос-
тойчивости судна в следующем порядке:
В результате приема груза приращение осадки составляет:
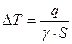 (7.9)
(7.9)
Где S – площадь действующей ватерлинии;

Новые значения аппликат центра величины и центра тяжести могут быть определены решением уравнений статических моментов объемов водоизмещения и веса судна относительно основной плоскости. В конечном итоге новая аппликата центра величины равна:
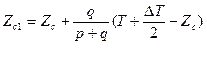 (7.10)
(7.10)
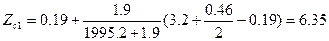
И новая аппликата центра тяжести равна:
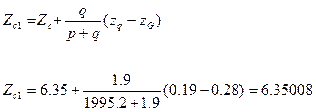 (7.11)
(7.11)
В формулах 7.10 и 7.11:
Zc и ZG- начальные аппликаты центра величины и центра тяжести;
Р- весовое водоизмещение груза до приема груза;
Zq- аппликата центра тяжести принятого груза q.
Новый метацентрический радиус:
Р1= р(1-q/p+q) (7.12)
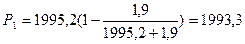
Новая метацентрическая высота
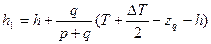 (7.13)
(7.13)
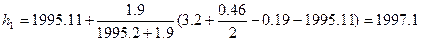
Коэффициент поперечной остойчивости судна после приема груза:
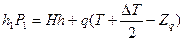 (7.14)
(7.14)
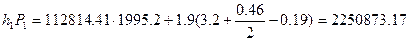
Библиографический список
1. Шолгунов Ю.В. Машины и оборудование лесозаготовок, лесосплава и
лесного хозяйства. Учебник для вузов / Ю. В. Шолгунов, Г.М. Кутуков,
Г.И. Ильин - М.: Лесная промышленность, 1982. - 520с.
2. Петров Я.П. Лесосплавной флот. Учебник для техникумов. - М.: Лесная
промышленность, 1972. - 200с.
3. Лебедев Н.И. Водный транспорт леса. Учебник для техникумов / Н.И.
Лебедев, Г.И. Поминова - М.: Лесная промышленность, 1987. - 368с.
Дата добавления: 2015-07-21; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вопрос 3. Классификация причин преступности. | | | Эксперт: Российский флот в 10 раз слабее американского |