
Читайте также:
|
1. Дайте определение математического ожидания случайной величины.
2. Для ряда распределения случайной величины x найдите математическое ожидание M (x); дисперсию D (x) и среднеквадратическое отклонение 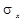 .
.
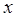
| |||||
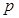
| 0,1 | 0,4 | 0,2 | 0,1 | 0,2 |
3. Перечислите основные свойства ковариации.
4. Докажите тождественность определений  .
.
5. Математическое ожидание случайной величины 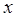 равно
равно 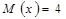 , дисперсия равна
, дисперсия равна 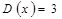 . Найдите математическое ожидание и дисперсию (если возможно) следующих величин:
. Найдите математическое ожидание и дисперсию (если возможно) следующих величин:
a. –3 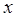 ; ;
| b. 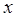 +1; +1;
| c. 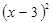 . .
|
6. Данные наблюдений за случайными величинами 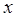 и
и 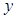 представлены в таблице:
представлены в таблице:
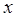
| ||||||
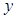
|
Необходимо нанести точки наблюдений на координатную плоскость, вычислить ковариацию и коэффициент корреляции, сделать выводы о линейной зависимости между переменными.
7. Рассчитанный по выборке переменных 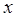 и
и 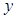 коэффициент корреляции оказался равным –1. Что можно сказать о линейной зависимости между переменными
коэффициент корреляции оказался равным –1. Что можно сказать о линейной зависимости между переменными 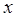 и
и 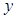 . Дайте графическую иллюстрацию.
. Дайте графическую иллюстрацию.
8. В модели линейной регрессии с убывающей тенденцией сумма квадратов остатков составила 250, а общая сумма квадратов составила 1000. Чему равен коэффициент детерминации модели? Поясните полученный результат.
9. 5. По десяти парам наблюдений получены следующие результаты:
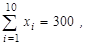
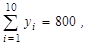
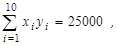
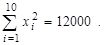
По методу наименьших квадратов оцените коэффициенты уравнения линейной регрессии 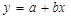 . Дайте интерпретацию полученных результатов.
. Дайте интерпретацию полученных результатов.
10. Для двух видов продукции А и В известны зависимости расходов предприятия y (тыс.руб.) от объема производства x (шт.):
11. 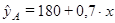 , ,
| 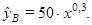
|
a.) Поясните смысл величин 0,7 и 0,3 в уравнениях регрессии.
b.) Сравните эластичность расходов от объема производства для продукции А и В при выпуске продукции А в 500 шт.
c.) Определите, каким должен быть выпуск продукции А, чтобы эластичность ее расходов от объема производства совпадала с эластичностью расходов на продукцию В.
12. Для статистической выборки, состоящей из 22 наблюдений, фактическое значение F-критерия Фишера составляет 48. Определите линейный коэффициент детерминации и поясните полученный результат.
13. По 14 предприятиям, производящим одинаковую продукцию, построена линейная регрессия зависимости объемов продаж от расходов на рекламу 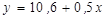 . Среднее квадратичное отклонение х равно 4,5. Среднее квадратичное отклонение у равно 3,2. Оцените качество модели с помощью F-критерия Фишера.
. Среднее квадратичное отклонение х равно 4,5. Среднее квадратичное отклонение у равно 3,2. Оцените качество модели с помощью F-критерия Фишера.
14. Изучается зависимость вида 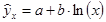 . После приведения модели к линейному виду, получены следующие суммы:
. После приведения модели к линейному виду, получены следующие суммы: 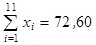
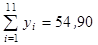
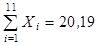
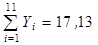
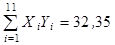
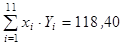
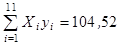
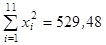
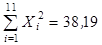 (где
(где 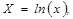
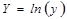 ). Оцените параметры уравнения регрессии
). Оцените параметры уравнения регрессии 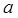 и
и 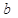 по МНК и, если возможно, дайте интерпретацию полученного уравнения.
по МНК и, если возможно, дайте интерпретацию полученного уравнения.
15. В уравнение регрессии для доходов населения вводится два качественных фактора: «пол» («муж.», «жен.»), образование («нач.», «сред.», «высш.») и место проживания («гор.», «сел.»). Сколько фиктивных переменных необходимо ввести в уравнение регрессии. Опишите эти фиктивные переменные.
16. По данным о темпах роста заработной платы в республике Татарстан за 10 месяцев 1999 года были оценены параметры основных трендов (в скобках указаны стандартные ошибки коэффициентов регрессии).
| Тип тренда | Уравнение | Коэффициент детерминации |
| Линейный | 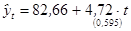
| 0,887 |
| Гиперболический | 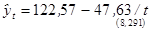
| 0,758 |
| Экспоненциальный | 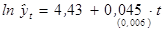
| 0,872 |
По каждому уравнению рассчитать скорректированный коэффициент детерминации. Дать интерпретацию линейного и гиперболического трендов. Выберите наилучший вариант уравнения тренда. По лучшему уравнению постройте точечный и интервальный прогнозы на ноябрь месяц (для уровня значимости 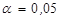 ;
; 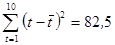 ).
).
| Номер года | Остатки | Номер года | Остатки | Номер года | Остатки |
| –0,7 | 0,9 | –0,1 | |||
| 0,0 | 0,0 | –0,2 | |||
| –0,2 | 0,3 |
Используя критерий Дарбина-Уотсона, проверить гипотезу о наличии автокорреляции в остатках (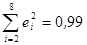 ;
; 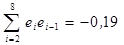 ). Сделайте выводы.
). Сделайте выводы.
| ||||||||
| … | … | … | … | … | … |
Рассчитать коэффициент автокорреляции уровней этого ряда первого порядка, если известно: 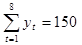 ;
; 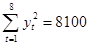 ;
; 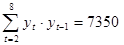 . Определите, включает ли исследуемый временной ряд тенденцию.
. Определите, включает ли исследуемый временной ряд тенденцию.
| Время года | Фактический объем продаж в 1996 г. | Компонента, полученная по аддитивной модели | ||
| Трендовая | Сезонная | Случайная | ||
| Зима | +4 | |||
| Весна | +5 | |||
| Лето | ||||
| Осень |
Определите недостающие в таблице данные, учитывая, что объем продаж компании ABC за 1996 год в целом составил 490 млн. руб.
20. Рассматривается система уравнений вида 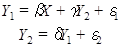 . Проверьте, является ли данная система идентифицируемой. Изменится ли ответ, если в число регрессоров второго уравнения включить: а) константу; б) переменную
. Проверьте, является ли данная система идентифицируемой. Изменится ли ответ, если в число регрессоров второго уравнения включить: а) константу; б) переменную 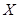 .
.
21. Дана эконометрическая модель денежного рынка:
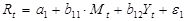 ,
,
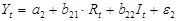 ,
,
где 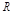 – процентная ставка; Y – ВВП; M – денежная масса; I – внутренние инвестиции; t – текущий период.
– процентная ставка; Y – ВВП; M – денежная масса; I – внутренние инвестиции; t – текущий период.
1) Определите, идентифицируемо ли каждое из уравнений модели.
2) Выберите метод оценки параметров модели.
3) Запишите приведенную форму модели.
22.Система эконометрических уравнений включает в себя следующие переменные (выберите несколько вариантов ответа):
□ Эндогенные;
□ Системные;
□ Экзогенные;
□ Случайные.
Дата добавления: 2015-07-21; просмотров: 477 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| МЕТОДИКА | | | Типы грузовых вагонов. |