Гранулометрический состав рудных материалов и методы его определения

Руды и продукты их переработки на различных стадиях рудоподготовки представляют собой сыпучие материалы, состоящие из кусков (зерен) различных размеров. Распределение кусков (зерен) по классам крупности (по их размеру) характеризует гранулометрический (или ситовый) состав сыпучих материалов.

Процесс разделения сыпучих материалов на отдельные классы (фракции) крупности называют классификацией по крупности. Такая классификация осуществляется:

1. разделением (грохочением) исходного материала на просеивающих поверхностях с калиброванными отверстиями (колосниковые решетки, сита,

решета и др.). Последовательный ряд размеров отверстий сит, применяемых для многократного грохочения, называется шкалой классификации, а отношение размеров отверстий смежных сит в закономерной шкале – модулем шкалы. При грохочении крупного и среднего по крупности материала чаще всего применяют модуль, равный 2. Такова, например, шкала классификации на средних ситах с отверстиями 50; 25; 12; 6 и 3 мм. Для мелких сит, применяемых для ситовых анализов небольших навесок, принимается меньший модуль.

2. разделением исходного материала на различные по крупности фракции в жидкой или газообразной среде, в которой взвесь минеральных частиц осаждается с различной скоростью в зависимости от их размеров и плотности. Такая классификация может быть гидравлической (водной) или пневматической (воздушной).

Для определения крупности материала применяют ситовый, седиментационный, микроскопический и другие методы анализа. Содержание относительно крупных классов (крупнее 0,074 или 0,044 мм) определяется рассевом пробы на ситах (ситовый анализ), а более тонких – с помощью седиментационного (шламового) и микроскопического анализов.

Ситовый анализ производится на механическом анализаторе (встряхивателе), состоящем из набора стандартных сит. Размеры наиболее распространенных контрольных сит с квадратными ячейками, применяемых в России и за рубежом, приводятся в таблице 27.

Результаты ситового анализа представляются различными способами. В частности, они могут быть представлены в виде таблиц. В качестве примера в таблице 28 приведены результаты ситового анализа пробы мелкой руды.

Классы крупности в таблицах записываются либо только “от–до”, либо “минус–плюс”, а суммарный выход записывают только по “плюсу” либо “по минусу”.

Таблица 27

Размеры квадратных ячеек контрольных сит в России и за рубежом

Россия	ФРГ	Франция	Велико-британия	США	Стандарт ИСО(ISO)
Размер, мм	Число меш*
0,040 0,045 0,050 0,056 0,063 0,071 0,080 0,090 0,100 0,112 0,125 0,140 0,160 0,180 0,200 0,224 0,250 0,280 0,315 0,355 0,400 0,450 0,500 0,560 0,630 0,700 0,800 0,900 1,00 1,25 - 1,60 - 2,00 - 2,50 - - - -	0,040 0,045 0,050 0,056 0,063 0,071 0,080 0,090 0,100 - 1,125 - 0,160 - 0,200 - 0,250 - 0,315 - 0,400 - 0,500 - 0,630 - 0,80 - 1,00 1,25 - 1,60 - 2,0 - 2,50 - 3,15 - 4,00	0,040 - 0,050 - 0,063 - 0,080 - 0,100 - 1,125 - 0,160 - 0,200 - 0,250 - 0,315 - 0,400 - 0,500 - 0,630 - 0,80 - 1,00 1,25 - 1,60 - 2,0 - 2,50 - 3,15 - 4,00	- 0,044 0,053 - 0,064 0,076 - 0,089 0,104 - 0,124 0,152 - 0,178 0,211 - 0,251 0,295 - 0,353 0,422 - 0,500 0,599 0,699 0,790 0,853 - 1,002 1,204 1,405 1,600 1,676 2,057 - 2,411 2,812 3,180 3,353 -	0,037 0,044 0,053 - 0,063 0,074 - 0,088 0,105 - 0,125 0,149 - 0,177 0,21 - 0,25 0,297 - 0,35 0,42 - 0,50 0,59 - 0,71 0,84 - 1,00 1,19 1,41 - 1,68 2,00 2,38 - 2,83 - 3,36 4,00	- - - - - - - - - - - -	0,040 0,045 0,050 0,056 0,063 0,071 0,080 0,090 0,100 0,112 0,125 0,14 0,16 0,18 0,20 0,224 0,25 0,28 0,315 0,35 0,40 0,45 0,50 0,56 0,63 0,71 0,80 0,90 1,00 1,25 1,40 1,60 1,80 2,00 2,24 2,50 2,80 3,15 3,55 4,00

* Число отверстий на 1 дюйм.

Таблица 28

Результаты ситового анализа пробы мелкой руды

Классы (фракции), мм	Выход отдельных классов	Суммарный выход по “плюсу” (суммарный остаток на сетках), %	Суммарный выход по “минусу” (суммарный просев), %
“от – до”	“минус-плюс”	весовой, кг	процентный, %
16 – 12 12 – 8 8 - 4 4 – 2 2 - 0	-16 +12 -12+8 -8+4 -4+2 -2+0	4,5 6,0 9,0 4,5 6,0	15,0 20,0 30,0 15,0 20,0	15,0 35,0 65,0 80,0 100,0	100,0 85,0 65,0 35,0 20,0
ВСЕГО:	30,0	100,0

При графическом изображении результатов ситового и шламового анализов получают так называемые характеристики крупности. Различают характеристики частные и суммарные, а также кривые распределения.

Частная характеристика отображает процентный выход отдельных классов в виде гистограммы, состоящей из серии прямоугольников, основаниями которых служат отрезки между размерами сит, ограничивающими данный класс, а высотой – отрезки, соответствующие процентным выходам классов. На рисунке 7.16 представлена частная характеристика ситового состава мелкой руды, показанного в таблице 28. На этом же рисунке приведена кривая распределения для этого ситового состава.

Кривая распределения отличается от частной характеристики тем, что выход классов относят каждый раз к одному и тому же интервалу оси абсцисс, а на оси ординат откладывают отношение выхода к интервалу. Если, например, на рисунке 7.16 за интервал принят узкий класс Δх = 1 мм, то распределение по интервалам 0-1 и 1-2 мм будет 20: 2 = 10 %; по интервалам 2-3 и 3-4 мм – 7,5 % и т.д.

Суммарные (кумулятивные) характеристики отображают суммарный выход классов по нарастающим итогам (рис. 7.17, по данным табл. 7.9). Применяют два способа суммирования: а) по “плюсу”, т.е. по суммарному остатку материала на ситах, начиная с самых крупных; и б) по “минусу” – по суммарному количеству материала в просеявшихся классах, начиная с самых мелких, т.е. по просеву.

Для аналитического выражения суммарной характеристики “по минусу” Андреевым и Шуманом было предложено уравнение:

(7.14)

где R – суммарный остаток на сите с отверстиями d, %;

(100 - R) – суммарный просев через то же сито, %;

d_max – размер максимального сита, на котором остаток равен нулю.

Показатель k характеризует степень кривизны характеристики: при k › 1 кривые суммарных остатков выпуклые, при k = 1 они – прямые линии; при k ‹ 1 кривые вогнутые, причем вогнутость их тем больше, чем меньше показатель k. Выпуклая характеристика “по плюсу” соответствует относительно малому количеству мелких классов и преобладанию крупных классов. Вогнутая кривая соответствует преобладанию мелких классов (рис.7.18). Для характеристик по просевам (“по минусу”) выпуклая кривая характеризует относительно большое количество мелких классов и относительно малое количество крупных.

Номинальной (или условной) максимальной крупностью продукта принято считать размер d_н отверстий того сита, на котором остаток составляет 5 %, т.е. R = 5 % (просев равен 95 %).

Уравнение (7.14) справедливо только для мелких классов продуктов дробления и измельчения. Поэтому для оценки крупности дробленых и в особенности измельченных продуктов широкое применение получило экспоненциально-степенное уравнение, предложенное Розиным и Рамлером:

, (7.15)

а также упрощенное уравнение В.А. Олевского:

,

где R – суммарный остаток на сите с диаметром отверстий d, %;

e – основание натуральных логарифмов;

m, m ₀ и n – постоянные, характерные для данных материалов.

В большинстве случаев куски дробленного или частицы измельченного материала имеют неправильную форму и при определении номинального размера кусочков или частиц их условно заменяют в каком-либо отношении эквивалентным телом правильной формы. Номинальным диаметром кусков и частиц, выделенных при ситовом анализе, считается диаметр круглого (или сторона квадратного) отверстия, определяющего размеры наибольших проходящих через него кусков.

Помимо определения крупности по номинальному (условному) диаметру крупность частиц неправильной формы оценивают одним линейным измерителем – “средним диаметром”, заменяющим все три измерения. В этом случае частица заменяется эквивалентным ей телом правильной геометрической формы. Понятие “средний диаметр” становится определенным лишь при условии, когда указано, в каком отношении устанавливается эквивалентность между измеряемой частицей и телом правильной формы. Например, “средний арифметический диаметр” частицы, близкой по форме к параллелепипеду, имеющий длину l, ширину b и толщину h, определяется как среднее арифметическое всех трех измерений по формуле:

(7.16)

Далее диаметр, найденный по формуле:

(7.17)

соответствует условию, что параллелепипедообразная частица заменяется кубом (с ребром d_r). Эквивалентность заключается в том, что объем такого куба равен объему правильного параллелепипеда, имеющего такие же размеры l, b и h, что и данная частица. В этом случае d_r называется среднегеометрическим диаметром.

Степень отклонения формы частицы от правильного шара оценивают коэффициентом сферичности Ψ, представляющим отношение поверхности шара S_ш к поверхности равновеликой по объему частицы S_r:

. (7.18)

Например, если частица имеет форму куба с ребром а, то отношение поверхности шара диаметром d к поверхности куба с ребром а будет:

(7.19)

Если эти тела равновелики по объему, то:

откуда:

Коэффициент сферичности куба можно определять после подстановки найденного значения а в предыдущее выражение (7.19):

Номинальный (средний) диаметр частиц какого-либо узкого класса (ограниченного размерами частиц d₁ и d₂) определяют как среднеарифметическое (полусумму) его пределов:

(7.20)

Имеются и другие формулы определения среднего диаметра частиц d_ср узкого класса.

Понятие “средний диаметр” (или “средневзвешенный диаметр”) применяют не только для узкого класса частиц, но и для всего продукта, состоящего из смеси частиц различных узких классов. Если какая-либо характерная физическая величина Z связана с диаметром d_i частиц кускового или порошковатого материала функциональной зависимостью типа:

Z = F (d_i),

то средневзвешенный диаметр D_ср того класса, которым при расчете заменяются все действительные классы крупности, должен быть определен из соотношения:

F (D_ср) Σ γ_i = Σ γ_i F (d_i), (7.21)

где D_ср – средневзвешенный диаметр для всего продукта в целом, мм; γ_i – выход узкого класса крупности, %;

Σ γ_i – общий выход всех классов (чаще всего Σ γ_i = 100 %), %;

d_i – диаметр, принимаемый за средний для данного узкого класса, мм.

Вид функции F (d_i) зависит от выбранного закона связи между параметрами Z и d_i. Сама функция F (d_i) носит название “определяющей функции”.

Имеется большое количество формул для вычисления среднего диаметра смеси частиц. На практике чаще всего используется средневзвешенный диаметр, вычисляемый по формуле:

(7.22)

или в развернутом виде:

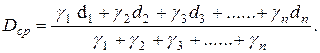(7.23)

Эквивалентный диаметр смеси зернистых материалов по своей газодинамической характеристике определяют по формуле:

(7.24)

Здесь D_э.з. – эквивалентный (средневзвешенный) диаметр смеси зерен по величине удельной поверхности, т.к. удельная поверхность обратно пропорциональна среднему диаметру узкого класса частиц (d_i).

Дата добавления: 2015-07-21