Типы несовместимости понятий

1) соподчинение, или координация, – отношение между непересека­ющимися понятиями, принадлежащими к общему роду:

А –береза, В – ель, С – дерево;

2) противоположность – отношение, фиксирующее максимальное отличие внутри рода: А –сильный, В –слабый;

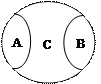
3) противоречие – отношение отрицания:

А –слабый, не- А – не-слабый ().

Закон обратного отношения между объемами и содержанием понятий – чем больше содержание понятия, тем меньше его объем, и наоборот. Так, если к содержанию понятия «треугольник» добавить новый признак «иметь равные стороны», то его содержание возрастет, а объем уменьшится, т.к. объем понятия «равносторонний треугольник» составляет лишь часть понятия «треугольник».

Логические операции с объемом понятия. Если объем одного понятия включается в объем другого, то первое понятие называется видовым, а второе – родовым. Переход от рода к виду представляет собой логическую операцию ограничения понятия (например: организм → растение), переход от вида к роду – опера­цию обобщения понятия (например: дерево → растение). Предел огра­ничения понятия – единичное понятие. Предел обобщения – уни­версальное понятие.

1. Обобщение. Логическая операция, в процессе которой производится переход от понятия с меньшим объемом к понятию с большим объемом, при этом содержание становится беднее. В основе операции – отношение подчинения. В пределе обобщение ведет к выработке всеобщего (универсального) понятия. При обобщении каждое последующее понятие должно быть ближайшим родом по отношению к предыдущему.

2. Ограничение. Логическая операция, в процессе которой производится переход от понятия с большим объемом к понятию с меньшим объемом, при этом содержание понятия становится богаче. Последовательно осуществляемое ограничение приводит к единичному понятию. При ограничении каждое последующее понятие должно быть ближайшим видом по отношению к предыдущему.

3. Деление понятия –логическая операция, раскрывающая объем понятия через перечисление его видов. Понятие, объем которого рас­крывается, – делимое. Виды, получающиеся в результате деления, – члены деления. Признак, по которому выделяются виды, – основание деления. Различают деление по видообразующему признаку (сту­денты: успевающие и отстающие) и дихотомическое (двучленное) де­ление, когда объем делимого понятия распадается на два противоре­чащих понятия (студенты: успевающие и неуспевающие). Логическая операция деления понятия образует основу классифика­ций, широко распространенных в естественных и технических науках.

Элементарные правила деления понятия

1. Деление должно быть соразмерным, т.е. объединение объемов поня­тий – членов деления должно в сумме давать объем делимого понятия. Нарушение правила соразмерности ведет к логической ошибке – непол­ному делению (например: «Люди бывают высокие и низкорослые»).

2. Деление должно производиться по одному основанию. Наруше­ние этого правила ведет к ошибке – делению с лишними членами (например: «Дети: воспитанные и наши»).

3.Члены деления должны исключать друг друга («Дети до 16 лет и подростки всех возрастов на кинофильм не допускаются» – данное деление нарушает это правило).

4. Деление понятий должно быть непрерывным и последователь­ным. Логическая ошибка в случае нарушения – сбивчивое деление. Дихотомическое деление всегда удовлетворяет правилам, поэтому оно чаще представлено в научных классификациях.

4. Сложение – логическая операция, в процессе которой из двух или нескольких понятий получается новое понятие с объемом, равным совокупному объему слагаемых.

а) Результатом сложения равнозначных понятий является одно из слагаемых: (А+В)=А или (А+В)=В. (Рис. 1);

б) результатом сложения понятий, находящихся в отношении подчинения, является большее по объему понятие: (А+В)=В. (Рис. 2);

в) результатом сложения понятий, находящихся в отношении пересечения объемов является множество, включающее все элементы А и все элементы В, включая и общую часть АВ: (А+В)=(АUD). (Рис. 3);

г) Результатом сложения несовместимых понятий является совокупное множество, куда входят все элементы множества А и все элементы множества В: (А+В)= (АUВ). (Рис.4).

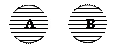
Рис.1	Рис.2	Рис.3	Рис.4

5. Умножением понятий называется логическая операция, в процессе которой из двух или нескольких понятий получается новое понятие, с объемом, равным общей части сомножителей.

а) Результатом умножения равнозначных понятий является один из сомножителей: (АхВ)=А или (АхВ)=В. (Рис.1);

б) результатом умножения понятий, находящихся в отношении подчинения является меньшее по объему понятие: (АхВ)=А. (Рис.2);

в) результатом умножения понятий, находящихся в отношении пересечения, является множество, представляющее общую часть сомножителей: (АВ). (Рис.3);

г) результат перемножения несовместимых понятий – пустое множество (О). (Рис.4).

Рис.1	Рис.2	Рис.3	Рис.4

6. Определение понятия –логическая операция, с помощью которой уточняется содержание понятия. Наиболее распространенная форма определения – указание на ближайший род определяемого понятия и видовое отличие. Определение понятия – сложная операция. Не все­гда удается дать четкое определение. В таких случаях прибегают к при­емам, заменяющим определение понятия: описанию –перечислению отдельных признаков; характеристике –выделению наиболее суще­ственных черт; непосредственному указанию на предмет; сравнению; номинальному определению – соглашению о смысле употребляемого термина.

В операции определения всегда соотносятся два понятия: опре­деляемое и определяющее. Определение будет явным, если оба поня­тия четко выражены: «Масса (определяемое) –мера инерции (опре­деляющее)».

Определение понятия через подведение определяемого под общий род и выделение видового отличия называется родовидовым определе­нием. Если в качестве видового отличия указан способ происхожде­ния, определение называется генетическим («Цилиндр – это фигура, образованная вращением прямоугольника вокруг одной из его сто­рон»). Если понятие определяется через перечисление операций, то определение будет операциональным.

Дата добавления: 2015-07-20