Катушка в цепи переменного тока

Соотношение между амплитудами тока I_L и напряжения U_L:

ω L I_L = U_L.

Ток отстает по фазе от напряжения на угол

Физическая величина X_L = ω L называется индуктивным сопротивлением катушки.

Теперь можно построить векторную диаграмму для последовательного RLC -контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I ₀. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC -контура изображена на рис. 2.3.2.

Векторная диаграмма на рис. 2.3.2 построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Из рисунка видно, что

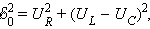
откуда следует

Из выражения для I ₀ видно, что амплитуда тока принимает максимальное значение при условии

Рисунок 2.3.3. Векторная диаграмма для последовательной RLC -цепи

или

Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC -цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

При последовательном резонансе (ω = ω₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают:

В § 2.2 было введено понятие добротности RLC -контура:

Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.

Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q

Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде ₀ напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми.

Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот.

d:\Program Files\Physicon\Open Physics 2.6. Part 2\design\images\buttonModel_h.gif

Модель. Вынужденные колебания в RLC -контуре

Дата добавления: 2015-07-20