Касательные и нормали

Производная – это предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Символически вычисление производной записывается следующим образом

.

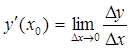Геометрический смысл производной выясняется при попытке решения задачи проведения через точку М₀ (х₀; у₀) касательной к графику функции y = f(x). Решение задачи состоит в том, что сначала проводят секущую, через точки М (х; у) и М₀, лежащие на графике. Приближение точки М к точке М₀ превращает секущую в касательную.

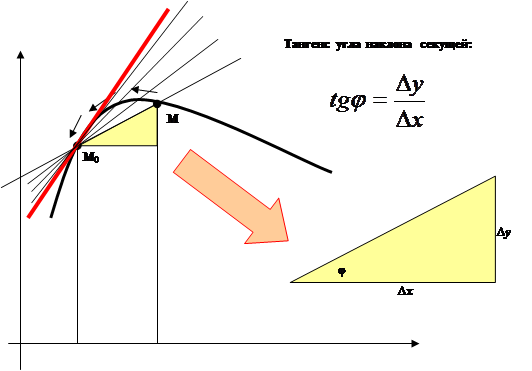Тангенс угла наклона секущей равен отношению приращения функции к приращению аргумента. При слиянии точек М и М₀ этот тангенс с одной стороны переходит в производную, а с другой – в тангенс угла наклона касательной. Итак, тангенс угла наклона касательной к графику функции равен производной функции в этой точке.

Выведем уравнение касательной к графику функции у = f(х) в точке (х₀; у₀), где у₀ = f(х₀). Касательная, как и любая другая прямая, имеет уравнение у = k х + b. Коэффициент k нам уже известен – он равен производной 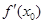. Остаётся определить значение свободного члена b. Поскольку касательная проходит через точку (х₀; у₀), то при подстановке этих координат в уравнение у = k х + b получится тождество у₀ = k х₀ + b. Отсюда следует, что b = у₀ – k х₀. В итоге мы получаем уравнение касательной: 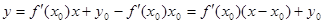. Приведём ещё один вариант записи уравнения касательной: .

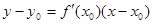При построении графика любой функции u = f₁(t) на отрезке [ t₀; t₁ ] мы можем рассуждать следующим образом:

· отрезок [ t₀; t₁ ] с помощью формулы x₀ = t (x₁ – x₀) отображается на экран. При этом отрезок [0; 1] отображается в полосу экрана, соответствующую экранным координатам х₀ и х₁;

· значения функции u с помощью формулы y₀ = u (y₁ – y₀) также отображаются на экран. При этом значения функции, заключённые между 0 и 1, отображаются в полосу экрана, соответствующую координатам у₀ и у₁. Однако график может выходить за пределы этой полосы, в том случае когда значения функции u становятся меньше 0 или больше 1;

· любая другая функция u = f₂(t) на том же отрезке [ t₀; t₁ ] строится аналогично, этой функцией может быть и касательная.

Задача 1. Построить на отрезке [–1; 1] график функции u = t² и касательную к нему в точке t₀ = 0,75. Точку касания выделить кружочком.

Решение. Производная функции u = t² в точке t₀ равна 2 t₀. Уравнение касательной имеет вид: u = 2 t₀ (t – t₀) + t₀². В одинаковых циклах строим и функцию и касательную.

screen 12 x0=320 y0=240 x1=520 y1=40 t0=.25 for t=–1 to 1 step.001 x=x0+t*(x1 – x0) u=t^2 y=y0+u*(y1–y0) pset(x,y),2 next t

k=2*t0 u0=t0^2 x=x0+t0*(x1–x0) u=k*(t0–t0)+u0 y=y0+u*(y1–y0) circle(x,y),2,1 for t=–1 to 1 step.001 x=x0+t*(x1– x0) u=k*(t–t0)+u0 y=y0+u*(y1–y0) pset(x,y),4 next t

Перпендикуляр, проведённый в точке касания к касательной, называется нормалью. Если k – тангенс наклона касательной, то вектор с координатами (1; k) направлен по этой касательной. Вектор с координатами (k; –1) перпендикулярен ему, поскольку их скалярное произведение равно нулю. Таким образом, тангенс наклона нормали равен –1/ k. Нормаль проходит через ту же точку, что и касательная. Пo этой причине уравнение нормали получается из уравнения касательной заменой k на –1/ k: .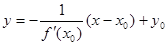

Задача 2. Достроить нормаль к графику из первой задачи.

Решение. Уравнение нормали имеет вид: u = – (t – t₀)/( 2 t₀) + t₀².

k=-1/k for t=-1 to 1 step.001 x=x0+t*(x1-x0) u=k*(t-t0)+u0 y=y0+u*(y1-y0) pset(x,y),4 next t

Легко понять, что нормали в точках, где производная обращается в нуль, являются вертикальными линиями. Фрагмент программы из задачи 2 в этом случае работать не будет, т. к. в нём будет выполнено деление на ноль. Чтобы обойти данную проблему, можно использовать параметрические уравнения прямой (и касательной, и нормали).

Поскольку направления касательной и нормали к графику любой функции u = f(t) в точке t₀ задаётся векторами (1; k) и (k; –1) соответственно (величина k равна производной данной функции в точке t₀), мы сразу можем записать параметрические уравнения касательной и нормали (параметр обозначим буквой р).

Касательная	Нормаль
t = t0 + p u= u0 +p k, где u0 = f(t0)	t = t0 + p k u= u0 – p, где u0 = f(t0)

Теперь мы можем построить нормаль и касательную, подвергнув величины t и u преобразованиям х = x₀ + t (x₁ – x₀) и у =y₀ + u (y₁ – y₀).

Задача 3. Построить на отрезке [–1,1; 1,1] график функции u = t³, а также касательные и нормали к нему в точках отрезка [–1; 1] с шагом 0,2.

Решение. Производная функции u = t³ в точке t₀ равна 3 t₀², т. е. k = 3 t₀². Параметр р, который заставляет точку двигаться по касательным и нормалям, изменяется в достаточно узких пределах от –0,3 до 0,3, чтобы укоротить изображаемые отрезки нормалей и касательных.

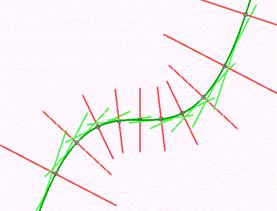
screen 12 x0=320 y0=240 x1=520 y1=40 for t0= –1 to 1.01 step.2 k=3*t0^2 u0=t0^3 x=x0+t0*(x1–x0) u=k*(t0–t0)+u0 y=y0+u*(y1–y0) circle(x,y),4,1 for p=–.3 to.3 step.001 t=t0+p u=u0+p*k x=x0+t*(x1–x0) y=y0+u*(y1–y0)

circle(x,y),1,10 next p for p=–.3 to.3 step.001 t=t0+p*k u=u0–p x=x0+t*(x1–x0) y=y0+u*(y1–y0) circle(x,y),1,12 next p next t0 rem График for t=–1.1 to 1.1 step.001 x=x0+t*(x1–x0) u=t^3 y=y0+u*(y1–y0) circle(x,y),1,2 next t

Длины отрезков нормалей и касательных растут при удалении от начала координат, поскольку возрастает производная. Попытаемся придумать способ, который позволит строить соответствующие отрезки так, чтобы они имели одинаковую длину. Для этого получим уравнение касательной, отнесённое к экранной системе координат.

Прежде всего, точка (t₀; u₀) уравнениями a₀ = х₀ + t₀ (x₁ – x₀) и b₀ = у₀ + u₀ (y₁ – y₀) преобразуется в точку (a₀; b₀). Далее, точка (t₀ +1; u₀ + k) теми же уравнениями a₁ = х₀ + (t₀ + 1)(x₁ – x₀) и b₀ = у₀ + (u₀ + k)(y₁ – y₀) преобразуется в точку (a₁; b₁).

Коэффициент наклона касательной на экране можно вычислить по формуле 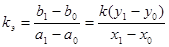. Если х₁ – х₀ = у₁ – у₀, т. е. если растяжение графика на экране по горизонтали и вертикали одинаково коэффициент наклона касательной не изменяется (k_э = k). Отметим, что для нормали экранный коэффициент наклона вычисляется по формуле 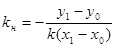. При задании различного масштаба по горизонтали и вертикали ортогональность на экране нарушается, т. к. произведение k_э k_н не равно –1.

В общем случае параметрические уравнения (параметр р) касательной на экране можно записать в виде:

х = а₀ + р,

у = b₀ + p k_э.

Однако длина вектора (1; k_э), задающего направление касательной всё ещё зависит от производной. Нормируем этот вектор, умножив на число обратное к длине этого вектора. В результате получим вектор (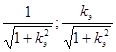). Он позволяет придать параметрическим уравнениям касательной вид

,

.

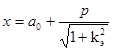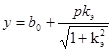Поскольку единичная длина на экране – это расстояние между соседними точками, то, изменяя параметр р от 1 до n, мы уложим в касательную n точек.

Задача 4. Построить на отрезке [–1,1; 1,1] график функции u = t³, а также отрезки касательных и нормалей к нему равной длины в точках отрезка [–1; 1] с шагом 0,2.

Решение. В программе из задачи 3 заменим цикл для построения касательных и нормалей. Параметр р, который заставляет точку двигаться по касательным и нормалям, изменяется в пределах от – 50 до 50.

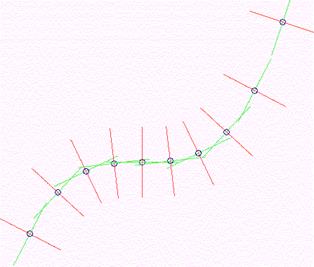
for t0=–1 to 1.01 step.2 ke=3*t0^2 u0=t0^3 a0=x0+t0*(x1–x0) b0=y0+u0*(y1–y0) circle(a0,b0),4,1 for p=–50 to 50 step 1 x=a0+p/sqr(1+ke^2) y=b0–p*ke/sqr(1+ke^2) pset(x,y),10 next p kn=–1/ke for p=–50 to 50 step 1 x=a0+p/sqr(1+kn^2) y=b0–p*kn/sqr(1+kn^2) pset(x,y),12 next p next t0

Дата добавления: 2015-07-20