Решение. Построим статический ряд Х

Построим статический ряд

Х

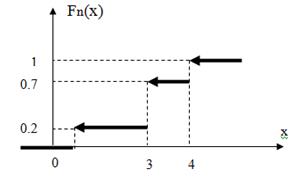
Свойства (совпадает со свойствами F(x)):

1.

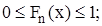
2.
3. – неубывающая по х;

4. – непрерывна слева.

Распределение и моменты э.ф.р. .

Введем индикаторную функцию . Тогда

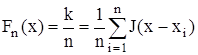, где при фиксированном значении х с.в.

J(x–X) ~B (1,p=F(x)), так как

J(x–X)
P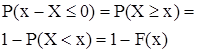

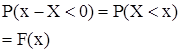
Известно, что тогда ~ , где p=F(x)

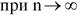
Таким образом, при фиксированном значении x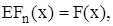

а это значит, что – несмещенная оценка для EX; а это значит, что – состоятельная оценка для F(x).

Сходимость к F(x).

а) Обозначим Воспользуемся неравенством Чебышева:

положим , тогда и

Получим при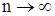

б) Воспользуемся теоремой Колмогорова. Если – последовательность независимых с.в. и выполнено условие то при т.е.

Положим 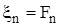и проверим условие теоремы Колмогорова

при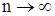

Докажем, что из сходимости п.н. 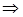сходимость п.в.

Дата добавления: 2015-07-20