Доказательство.

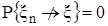Пусть т.е. или

Хотя бы при одном , а сходимость п.в. означает, что

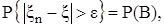но и требовалось доказать, т.е.

Замечание. Из доказанного утверждения следует, что т.к. при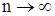

по теореме Колмогорова, то что было установлено раньше непосредственно по неравенству Чебышева.

Точность и надежность для F(x) при фиксированном значении х.

а) Пусть n велико. Тогда по следствию из интегральной теоремы Муавра – Лапласа

Здесь Р – надежность оценки для F с точностью ε, а – нижняя граница надежности.

б) При любом n по неравенству Чебышева имеем – нижняя граница надежности оценки для F с точностью ε.

Дата добавления: 2015-07-20