Расчет зубчатых колес по контактным напряжениям

Расчет зубчатых колес заключается в определении параметра контактных на­пряжений :

, (2.20)

где: 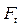– расчетная окружная сила в зубчатом зацеплении, Н;

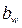– рабочая ширина зуба при расчете контактных напряжений, мм;

– начальный диаметр шестерни, мм;

– единичное контактное напряжение;

– коэффициент учитывающий перекрытие зубьев;

– коэффициент, учитывающий распределение нагрузки между зубьями в зависимости от степени точности передачи;

– коэффициент, учитывающий распределение нагрузки по ширине венца;

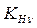– коэффициент, учитывающий динамическую нагрузку, возникшую в заце­плении;

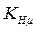– коэффициент, учитывающий влияние трения и смазки;

– коэффициент, учитывающий влияние размеров зубчатого колеса и мо­дуля зубьев;

Определяем расчетную окружную силу :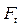

, (2.21)

где: 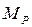– расчетный момент на ведущем валу, Н;

– начальный диаметр шестерни, мм;

– число пар зубчатых колес, одновременно находящихся в зацеплении;

Расчетный крутящий момент на ведущем валу коробки передач 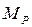определя­ется по формуле:

, (2.22)

где: , , , 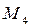– крутящие моменты на ведомом валу коробки передач на каждой передаче, Н·м;

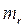– показатель кривой выносливости;

, , , – приведенное число циклов нагружения на каждой передаче за весь период эксплуатации;

– суммарное число циклов нагружения за весь период эксплуатации;

Крутящие моменты на ведомом валу коробки передач на i -й передаче 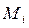опре­деляются по формуле:

, (2.23)

;

;

;

;

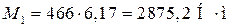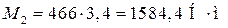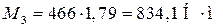При расчете зубчатых колес коробки переключения передач на контактную выносливость принимаем показатель кривой выносливости [3].

Приведенное число циклов нагружения на i -й передаче определяется по формуле:

, (2.24)

где: – расчетная частота вращения ведомого вала коробки передач на i -й пере­даче, ;

Расчетную частоту вращения ведомого вала коробки передач на i -й передаче берем из табл. 2.2:

;

;

;

;

.

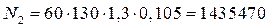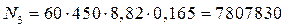Суммарное число циклов нагружения за весь период эксплуатации опреде­ляется по формуле:

, (2.25)

;

Расчетный крутящий момент для шестерни 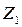равен:

;

Расчетный крутящий момент для шестерни привода промежуточного вала

Передаточное число зацепления 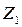- определяется по формуле:

, (2.26)

где: – число зубьев шестерни;

– число зубьев колеса;

Число зубьев шестерни и колеса [6].

;

Определяем рабочую ширину зубчатого венца. Принимаем . Для зацепления повышенной передачи раздаточной коробки ширина зубчатого венца , [6].

Определяем начальные диаметры шестерни и зубчатого колеса.

Начальные диаметры цилиндрической шестерни и цилиндрического ко­леса вычисляются по формулам:

, (2.27)

, (2.28)

где: – межосевое расстояние, мм;

Межцентровое расстояние шестерни и колеса повышающей передачи .

;

;

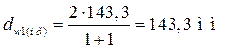Число пар зубчатых колес зацепления .

Расчетная окружная сила в зацеплении:

;

Определение единичного контактного напряжения .

Единичные контактные напряжения :

, (2.29)

где: – угол зацепления в нормальном сечении;

Угол зацепления в нормальном сечении определяется по формуле:

, (2.30)

где: – окружной модуль, мм;

– угол профиля в торцевом сечении;

Для цилиндрической косозубой передачи: и , где: – нормальный модуль; – угол профиля зуба в нормальном среднем сече­нии, -угол наклона зубьев [1].

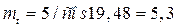
Угол зацепления в нормальном сечении для зацепления:

;

Единичные контактные напряжения в зацеплении:

;

Определение коэффициента, учитывающего перекрытие зубьев .

Для косозубых передач коэффициент, учитывающий перекрытие зубьев оп­ределяют по нанограммам [3] в зависимости от значения коэффициентов осевого 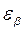и торцевого 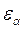перекрытия.

;

,

;

где: ;

;

;

;

;

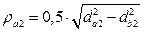где: , - диаметры вершин зубьев шестерни и колеса соответственно.

;

;

;

;

Следовательно по монограмме

Определение коэффициента , учитывающего распределение нагрузки ме­жду зубьями в зависимости от степени точности передачи.

Коэффициента , учитывающего распределение нагрузки между зубьями в зависимости от степени точности передачи определяется по формуле:

, (2.31)

где: , – коэффициенты, учитывающие непостоянство интенсивности на­грузки на наклонных контактных линиях и влияние точности изготовления на распределение нагрузки между зубьями соответственно.

Для косозубых передач 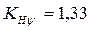т.к. 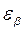>1,0 [3]. А значение находят по рис. 1.7 [3] в зависимости от степени точности передачи, нормы плавности ра­боты и расчетной работы и расчетной окружной скоростью в зацеплении.

где: расчётная частота вращения зубчатого колеса.

;

Расчетная окружная скорость в зацеплении:

;

;

Определение коэффициента , учитывающего распределение нагрузки по ширине венца.

Коэффициент , учитывающий распределение нагрузки по ширине венца определяют:

для передач с неразветвленным потоком мощности – передача:

, (2.32)

где: – коэффициент, учитывающий распределение нагрузки по ширине венца в начальный период работы передачи;

– коэффициент, учитывающий приработку зубьев в процессе эксплуата­ции;

– коэффициент, учитывающий неравномерность распределения нагрузки между разветвлениями в начальный период работы передачи.

Для нахождения коэффициента используем зависимость , при­веденную на рис.1.8 [3,стр.8], где определяется по формуле:

, (2.33)

Для зацепления - :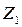

;

По зависимости определяем

Коэффициент, учитывающий приработку зубьев в процессе эксплуатации определяем по табл. 1.2 [3,стр. 9] в зависимости от расчетной окружной скоро­сти 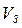, м/с.

Коэффициент, учитывающий приработку зубьев в процессе эксплуатации: для зацепления - при твердости активных поверхностей зубьев 60HRC ;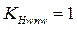

Коэффициент для передачи:

;

Определение коэффициента 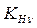, учитывающего динамическую нагрузку, воз­никшую в зацеплении.

Определение коэффициента 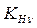, учитывающий динамическую нагрузку, воз­никшую в зацеплении:

, (2.34)

где: – коэффициент внутренней динамической нагрузки;

– коэффициент, учитывающий влияние внешних динамических нагрузок;

Коэффициент , учитывающий влияние внешних динамических нагрузок оп­ределяем по рис. 1.10[3,стр. 11]. Коэффициент для зацепления:

;

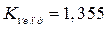, (2.35)

где: – внутренняя динамическая нагрузка, Н;

Внутренняя динамическая нагрузка определяется как:

, (2.36)

где: – внутренняя динамическая нагрузка при расчетном значении окружной скорости, Н;

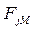– предельное значение динамической нагрузки, Н;

Внутренняя динамическая нагрузка при расчетном значении окружной ско­рости определяется по формуле:

, (2.37)

где: – внутренняя динамическая нагрузка при окружной скорости 1м/с, Н;

Внутренняя динамическая нагрузка при окружной скорости 1м/с опре­деляется по формуле:

,

где: – коэффициент, учитывающий тип передачи;

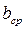– средняя ширина венца шестерни и зубчатого колеса, мм;

– расчетная производственная погрешность зубчатых колес, мкм;

Для косозубой цилиндрической передачи коэффициент, учитывающий тип передачи .

По табл. 1.4 [3,стр. 10] определяем расчетная производственная погрешность зубчатых колес. Для данных зубчатых колес при степени точности по нормам плавности 7 определяем .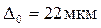

Средняя ширина венца шестерни и зубчатого колеса 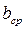определяется по фор­муле:

(2.38)

Определяем среднюю ширину шестерни 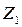и колеса :

;

Определяем внутреннюю динамическую нагрузку при окружной скорости 1м/с для зацепления:

;

Определяем внутреннюю динамическую нагрузку при расчетном значении окружной скорости для зацепления:

;

Предельное значение динамической нагрузки 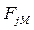для косозубой цилиндриче­ской передачи определяется по формуле:

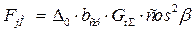; (2.39)

где: 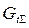а – суммарная удельная жесткость сопряженных зубьев, Н/(мм·мкм);

Для косозубой передачи суммарная удельная жесткость сопряженных зубьев [3, стр. 10].

Определяем предельное значение динамической нагрузки для передачи - :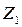

;

Сопоставляем значения 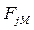и и меньшее из них принимаем в качестве рас­четного значения внутренней динамической нагрузки . Так для зацепления - принимаем .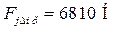

Определяем коэффициент внутренней динамической нагрузки для зацепле­ния:

;

Определяем искомое значение коэффициента 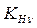, учитывающий динамиче­скую нагрузку, возникшую в зацеплении:

;

Определение коэффициента 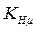, учитывающего влияние трения и смазки.

При использовании смазочных материалов, рекомендуемых для агрегатов трансмиссии автомобиля [3, стр. 11].

Определение коэффициента , учитывающего влияние размеров зубча­того колеса и модуля зубьев.

Для зубчатых колес, имеющих начальный диаметр [3, стр. 11].

Определяем искомое значение контактных напряжений для шестерни 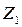нахо­дящейся в зацеплении:

;

Результаты расчета зубчатых колес на сопротивление усталости по контакт­ным напряжениям представлены в табл. 2.5.

Таблица 2.5

Результаты расчета зубчатых колес на сопротивление усталости по контактным напряжениям

Коэффициент	Обозначение	Значение
Расчетная окружная сила в зубчатом зацеплении, Н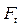
Рабочая ширина зуба при расчете контактных на­пряжений, мм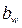
Начальный диаметр шестерни, мм		143,3
Единичное контактное напряжение		5,51
коэффициент учитывающий перекрытие зубьев		0,671
Коэффициент, учитывающий распределение на­грузки между зубьями в зависимости от степени точности передачи		1,56
Коэффициент, учитывающий распределение на­грузки по ширине венца		1,155

Окончание таблицы 2.5

Коэффициент	Обозначение	Значение
Коэффициент, учитывающий динамическую на­грузку, возникшую в зацеплении		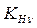1,49
Коэффициент, учитывающий влияние трения и смазки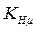
Коэффициент, учитывающий влияние размеров зуб­чатого колеса и модуля зубьев
Расчетное контактное напряжение, МПа		13,94

Дата добавления: 2015-07-20