Парабола

План

1. Коло.

2. Еліпс.

3. Дослідження рівняння еліпса.

4. Гіпербола.

5. Дослідження рівняння гіперболи.

6. Парабола.

7. Дослідження рівняння параболи.:

Ключові поняття і терміни:

- коло, еліпс, гіпербола, парабола.

Література:

1. Грисенко М.В., Математика для економістів.-К.: «Либідь»,- 2007р.,

стор. 124-129.

2. Рудавський Ю.К., Костробій П.П., Д.В.Уханська, Лінійна алгебра та аналітична геометрія.-Л.: «Бескід Біт»,-2002р., стор. 113-125.

3. Овчинников П.П., Яремчук Ф.П., Михайленко В.М., Вища математика, ч.1.,-К.: «Техніка»,-2003р., стор. 141-158.

4. Лейфура В.М., Голодницький Г.І., Файст Й.І., Математика.-К.: «Техніка», -2003р., стор. 133-155.

5. Пономаренко О.І., Перестюк М.О., Бурим В.М., Основи математичної економіки.-К.: «Інформ техніка», -1995р.

Криві другого порядку

Лінії, координати точок яких задовольняють рівняння, що в прямокутній системі координат є рівнянням другого степеня, називають лініями, або кривими, другого порядку. До них належать коло, еліпс, гіпербола, парабола.

Коло

Означення. Колом називають геометричне місце точок площини, рівновіддалених від заданої точки – центра кола – на задану відстань – радіус кола.

Виведемо рівняння кола. Нехай задано коло з центром у точці С (a; b) і радіусом R. Візьмемо на колі довільну точку М (х; у) (рис. 1). Тоді за означенням кола СМ = R, тобто

СМ = √(x – a)² + (y – b)² = R,

або

(х – а)² + (у – b)² = R². (1)

належать колу. Рівняння (1) є канонічним рівнянням кола.

Якщо центр кола знаходиться в точці (0;0), то рівнянням має вигляд

х² + у² = R². (2)

2.Еліпс

Означення. Еліпсом називають геометричне місце точок площини, сума відстаней від яких до заданих точок (фокусів) є сталою й більшою за

Виведемо рівняння еліпса. Через F_1, F₂ позначимо фокуси, 2_с - відстань між ними, 2_а - суму відстаней від довільної точки еліпса до фокусів. За означенням 2_а > 2_с , тобто а > с.

Через точки F_1,F₂ проведемо вісь абсцис, а вісь ординат спрямуємо так, щоб вона проходила через середину відрізка F_1, F₂ перпендикулярно до осі Ох (рис. 2).

У вибраній системі координат F₁(-c;0), F₂ (c;0). Виберемо на еліпсі довільну точку М (х; у). За означенням еліпса F₁ М + F₂ М = 2_а.

Оскільки F₁ М =√ (х + с)² +(у – 0)² і F₂ М =√ (х – с)² + (у – 0)² , то маємо рівняння еліпса

√(х + с)² + (х – с)² + √(х – с)² + у² = 2_а.

Спростимо це рівняння, перенісши один корінь у праву частину й піднісши до квадрата обидві частини рівності:

√(х + с)² + у² = 2_а – √(х – с)² + у²,

(х + с)² + у² = 4_а - 4_а (х – с)² + у² + (х – с)² + у²,

х ² + с² = 4_а² – 4_а √ (х – с) + у² +х² – 2_сх + с²,

4_а √ (х – с)² + у² = 4_а² – 4_ах ,

а√ (х – с)² + у² = а² – сх..

Знову піднесемо обидві частини рівності доквадрата:

а² х² – 2а²сх + а² х² + у²с² = а⁴ – 2а² сх + с² х²,

(а² – с²)х² + а²у² = а²(а² – с²).

Поділимо обидві частини на а²(а² – с²):

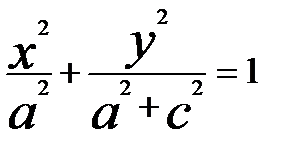
За означенням еліпса а² > с². Позначимо b² = а² – с². Тоді рівняння матиме вигляд

, а > b. (3)

Дослідження рівняння еліпса дає змогу зробити висновок, що параметри а і b є довжинами півосей еліпса, які розташовані на осях координат.

Вершинами еліпса, є точки А ₁ (а; 0), А₂ (а; 0), B(0; b), B₂ (0;b).

Відрізки А₁А₂ = 2а і В₁В₂ = 2b утворюють відповідно велику й малу осі еліпса.

Якщо фокуси еліпса лежать на осі Оу (рис. 2), то його канонічне рівняння має вигляд

, а > b.

Фокусами цього еліпса є точки F₁ (0; -с) і F₂ (0; с), вершинами – точки А₁ (0; - а), А₂ (0; а), В₁ (-b; 0), B₂ (b; 0), і відрізки А₁ А₂ = 2а і В₁ B₂ = 2b утворюють відповідно велику й малу осі еліпса.

Ексцентриситетом еліпса називають величину e = c/a. Оскільки за означенням еліпса a > c, то 0 < e < 1.

Ураховуючи співвідношення між параметрами c² a² - b² маємо

с ² а² – b² b

е² = а² = a² = 1 - a,

тому

b = √1 – е²

а

З останнього рівності випливає геометрична інтерпретація ексцентриситету. При е числа а і b майже рівні, тому еліпс близький до кола, причому для кола e = 0. Якщо е близький до 1, то число b дуже мале порівняно з числом a, і еліпс сильно «витягнутий» уздовж великої осі. Таким чином, ексцентриситет еліпса характеризує його форму.

3. Гіпербола

Означення. Гіперболою називають геометричне місце точок площини, для яких модуль різниці відстаней до двох заданих точок (фокусів) є величиною сталою й меншою, ніж відстань між фокусами.

Виведемо рівняння гіперболи. Виберемо систему координат таким чином, щоб вісь Ох проходила через фокуси F₁ і F₂, а вісь Оу – через середину відрізка F₁ F₂ перпендикулярнодо нього. Тоді у вибраній системі координат F₁ (-c; 0) і F₂ (c; 0). Візьмемо на гіперболі довільну точку M(х; у) ( рис 3).

За означенням гіперболи відстань між 2 c більша за різницею відстаней до фокусів 2 а, тому а < с і маємо F₁ M – F₂M = 2а, F₁ M – F₂M = ±2 a, Отже,

√(х + с)² + у² - √(х – с)² + у² = ± 2а.

Аналогічно, як і у випадку еліпса можна перетворити рівняння (що пропонується зробити самостійно) й звести його до вигляду

х² - у² = 1

а² а² – с²

Для гіперболи за означенням с² > а². Позначимо b² = c² – a². Тоді рівняння гіперболи матиме вигляд

х² - у² = 1. (5)

а² b²

Це канонічне рівняння гіперболи, фокуси якої лежать на осі Ох (рис. 3).

Дослідження рівняння гіперболи дає змогу визначити властивості гіперболи й побудувати її (рис. 3 а).

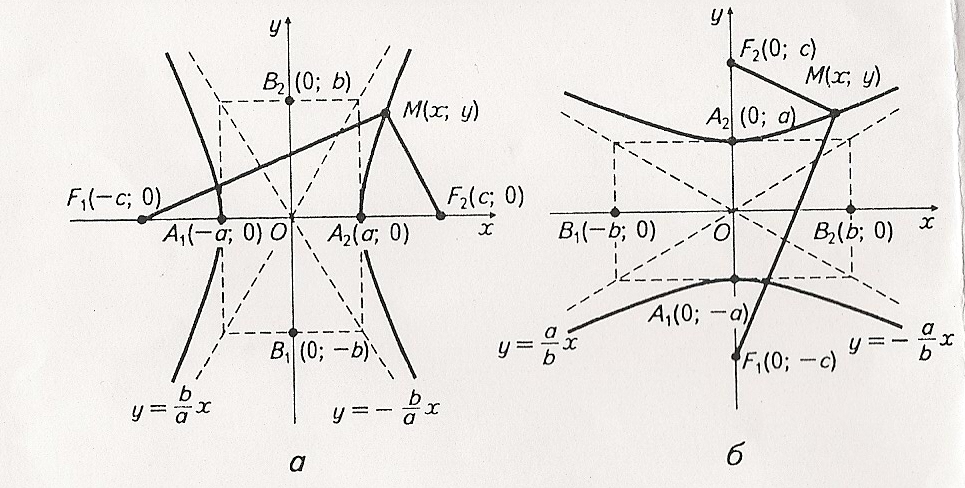
Точки А₁ (-а; 0) і А₂ (а; 0) називають вершинами гіперболи. Відрізок А₁ А₂ = 2а утворює дійсну вісь гіперболи, а відрізок В₁В₂ = 2b – її уявну вісь. Прямі у = ± b х

a є асимптотами гіперболи. Ексцентриситет гіперболи е = с/а > 1 характеризує її форму.

Якщо фокуси гіперболи лежать на осі Оу (рис. 3 б), то її канонічне рівняння має вигляд ,

а рівняння асимптот

Якщо дійсна та уявна осі гіперболи рівні, то гіперболу називають рівносторонньою.

Парабола

Означення. Параболою називають геометричне місце площини, відстані від яких до заданої точки (фокуса) й заданої прямої (директриси) рівні.

Виведемо рівняння параболи. Виберемо систему координат таким чином, щоб вісь Ох проходила перпендикулярно до директриси через фокус параболи – точку F. За початок координат візьмемо точку О, що є серединою відрізка FN (рис. 4). Відстань між фокусом і директрисою позначають р. Тоді

фокус параболи F (р/2; 0), а рівняння директриси х = - р/2.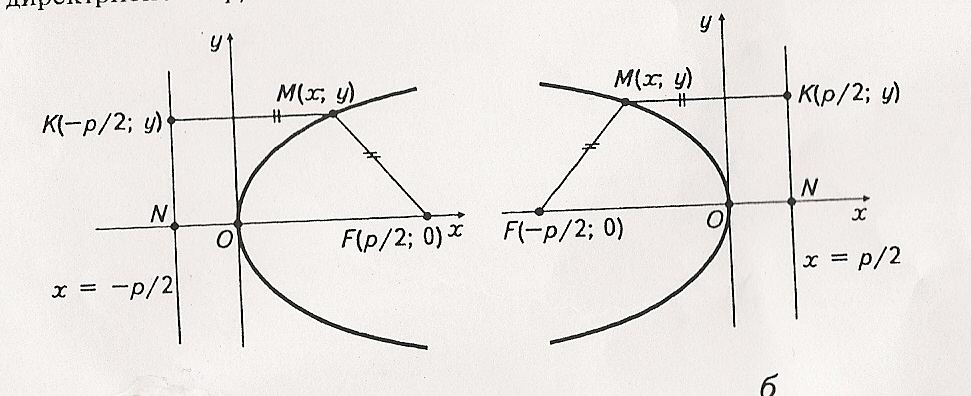

Виберемо на параболі довільну точку М(х; у). За означенням FM = KM. Оскільки

FM = √ (х – р/2)² + у², КМ = √(х + р/2)² = х + р/2,

т о

х + р/2 = √ (х + р/2)² + у².

Піднісши до квадрата обидві частини рівності й здійснивши перетворення (пропонується зробити це самостійно), матимемо рівняння

у² = 2рх, р> 0, (7)

яке називають канонічни м рівнянням параболи, симетричної відносно осі Ох, із вершиною в початку координат і вітки якої направлені вправо (рис. 4).

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є Ох і вітки направлені вліво (рис. 4 б), має вигляд

у² =-2рх, р> 0. (8)

Координати її фокуса F(-р/2;0), а рівняння директриси х = р/2. Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки якої направлені вгору (рис. 5 а), має вигляд

х² = 2рх, р > 0. (9)

Координати її фокуса F (0; р/2), а рівняння директриси у = - р/2

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки якої направлені вниз (рис. 5 б), має вигляд

х² = - 2рх, р > 0. (10)

Координати її фокуса F(0; -р/2), а рівняння директриси у = р/2.

---

Дата добавления: 2015-07-20