Схемы из функциональных элементов

Представлению функций алгебры логикиможно придать некоторый «инженерно-конструктивный» смысл. Можно рассматривать формулу Ф (х_1, х_{2 ……….} x_n) над каким-то произвольным фиксированным множеством элементарных функций F как «черный ящик», некое устройство, на вход которого подаются всевозможные наборы значений логических переменных, а на выходе появляются соответствующие этим наборам значения функции f, представляемой формулой Ф (рис.25)

x ₁

. f (x ₁ ,…,x _n)

.

.

x _n

Рисунок 25

«Черный ящик» функционирует как процесс построения формулы из подформул, добираясь

при этом до «базисных» формул из множества F, которые являются структурными элементами,

из которых собран «черный ящик», вычисляющий функцию f.

Базисом на множестве элементарных функций F для булевой алгебры являются: конъюнкция, дизъюнкция и отрицание. Структурные элементы, соответствующие этим операциям называются соответственно: конъюнктор, дизъюнктор и инвертор и могут быть изображены как показано на рис.26

a б в

Рисунок 26

Например формулу можно представить следующей схемой из функциональных элементов (рис.27)

x ₁

x ₁ ~ x ₂

x ₂

Рисунок 27

Математически «схема» определяется как ориентированный граф специального вида, в котором и вершины и дуги снабжены некоторыми метками.

Пусть фиксированы множества: F (булевых функций) и X (булевых переменных).

Схемой из функциональных элементов над базисом F È X (СФЭ), или просто схемой над базисом F È X, также (F,X)-схемой, называют бесконтурный ориентированный граф (т.е. сеть), каждая вершина которого помечена одним из элементов множества F È X.

При изображении схем входы обозначаются кружочками, а вершины, не являющиеся входами, - треугольниками, внутри которых записано обозначение функции, помечающей данную вершину. Выходы отмечаются «выходными» стрелками.

УКАЗАНИЯ

Перед решением задач контрольной работы рекомендуется ознакомиться со следующими методическими указаниями:

1. Белоусов А.И., Ткачев С.В. Дискретная математика: Учеб. для вузов/ под. ред. В.С. Зарубина, А.П. Крищенко.- М.: Изд-во МГТУ им. Н.Э.Баумана, 2001. – 744 с.

2. Пономарев В.Ф. Основы дискретной математики. Учебное пособие. -Калининград: КГТУ, 1997.– 152 с.

ЗАДАНИЕ: Опираясь на законы булевой алгебры, представить в видесхем из функциональных элементов формулы булевой алгебры

Вариант № 1.

Вариант № 2.

Вариант № 3.

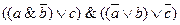
Вариант № 4.

Вариант № 5.

Вариант № 6.

Вариант № 7.

Вариант № 8.

Вариант № 9.

Вариант № 10.

Вариант № 11.

Вариант № 12.

Вариант № 13.

Вариант № 14.

Вариант № 15.

Вариант № 16.

Вариант № 17.

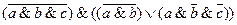
Вариант № 18.

Вариант № 19.

Вариант № 20.

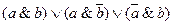
Вариант № 21.

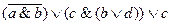
Вариант № 22.

Вариант № 23.

Вариант № 24.

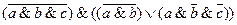
Вариант № 25.

Дата добавления: 2015-07-20