Задание 8

Построить связанный ориентированный граф, имеющий как минимум две центральные вершины, как минимум две периферийные вершины, как минимум две обычные вершины так, чтобы его радиус был не равен нулю и не равен диаметру. Начать построение с 6 вершин, добиться результата добавлением и удалением дуг и вершин. Построить максимальное покрывающее деревократчайших путей.

В отчете представить построенный граф с выделенным деревом, центром и периферией, над вершинами надписать их эксцентриситеты, указать значения радиуса и диаметра графа.

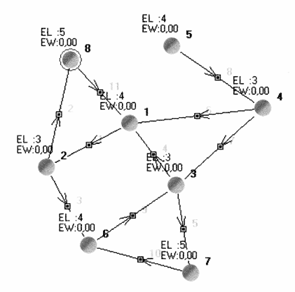
Рисунок 22

Эксцентриситеты вершин:

ехс(1)=4; ехс(2)=3; ехс(3)=3; ехс(4)=3;

ехс(5)=4; ехс(б)=4; ехс(7)=5; ехс(8)=5.

Центральные вершины:

2, 3, 4 (ехс=3).

Периферийные вершины:

7, 8 (ехс=5).

Обычные вершины:

1, 5, 6 (ехс=4).

Радиус графа:

R=exc(2)=ехс(3)=ехс(4)=3¹0.

Диаметр графа:

D=exc(7)=ехс(8)=5¹R.

Вывод:

В данной лабораторной работе были изучены различные способы представления графов и методы исследования топологических структур с использованием основных положений теории графов.

Дата добавления: 2015-07-20