Приложение вычетов к вычислению некоторых действительных интегралов

Многие определенные интегралы, и особенно несобственные, довольно просто вычисляются с помощью теории вычетов.

Суть метода состоит в переходе в интеграле от действительной к комплексной переменной.

Пусть надо вычислить интеграл от действительной функции по какому-нибудь отрезку действительной оси. Тогда дополняют отрезок некоторой кривой в плоскости комплексной переменной так, чтобы образовался замкнутый контур, ограничивающий некоторую область D.

Рассматривают функцию . Применяя к ней основную теорему о вычетах и, следовательно, находят

,

где сумма вычетов функции относительно всех особых точек, лежащих в области D.

Если удается вычислить интеграл , то задача вычисления интеграла будет решена.

1. Рассмотрим следующий определенный интеграл

,

где − рациональная функция от и .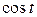

Пусть , если положить , где , тогда , , , .

Тогда

, (78)

где есть сумма вычетов функции 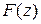относительно полюсов, заключенных внутри окружности .

2. Рассмотрим следующий интеграл

,

где − рациональная функция от :

.

Предполагаем, что степень многочлена в числителе дроби меньше степени знаменателя по крайней мере на две единицы, и знаменатель дроби не имеет действительных корней.

Если рациональная функция не имеет полюсов на вещественной оси, то

(77)

где – нули , лежащие в верхней полуплоскости ().

Пример 1. Вычислить интеграл .

Применяя , получаем после преобразований

.

Внутри единичного круга при условии находится только один полюс (двукратный) .

Вычет функции относительно этого полюса и .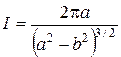

Пример 2. Вычислить интеграл .

Подынтегральная функция – четная, поэтому

Для функции – многочлены второй и четвертой степени и . Нули функции и лежат вне вещественной оси, причем в верхней полуплоскости лежит лишь нуль . Условия формулы (77) выполнены для данной функции, и, следовательно, и .

Дата добавления: 2015-07-20