Первый закон термодинамики

Вся тепловая энергия (теплота), подведенная к системе, расходуется на изменение ее внутренней энергии и на совершение работы.

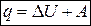(1.14)

или

dq > 0 положительная теплота;

dq < 0 отрицательная теплота.

1.4. Термодинамические процессы идеальных газов.

1. Политропный процесс – изменяются параметры рабочего тела при постоянной теплоемкости и отсутствии движения.
2. Изохорный процесс – процесс, протекающий при постоянном объеме рабочего тела.
3. Изоборный – процесс, протекающий при постоянном давлении рабочего тела.
4. Изотермический – процесс, протекающий при постоянной температуре рабочего тела.
5. Изоэнтальпийный или адиабатный –процесс, протекающий без теплообмена между рабочим телом и внешней средой.

I. Изохорный процесс

Пример: охлаждение и нагревание

газа в в герметичном сосуде.

Рис. 1.3. Изохорный процесс в PV – диаграмме

График – изохора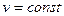

, Поделим 1-е уравнение на 2-е:

Давление изменяется прямо пропорционально температуре газа.

Уравнение 1-го закона термодинамики

В изохорном процессе вся подведенная теплота идет на увеличение внутренней энергии.

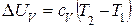(1.15)

II. Изобарный процесс.

Рис. 1.4. Изобарный процесс в PV – диаграмме

Пример: процесс нагревания воздуха в негерметичном помещении.

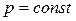
График – изобара.

Из уравнения состояния газа следует:

Объем газа изменяется прямо пропорционально его температуре.

В изобарном процессе теплота, подведенная к рабочему телу,

расходуется на изменение внутренней энергии тела и на

совершение работы.

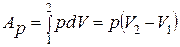или

т.к. и т.е.

универсальная газовая

постоянная

Если принять, что , то R это работа, производимая 1 кг газа при его нагревании на 1⁰С в изобарном процессе.

(1.16)

или

Энергию, равную сумме внутренней энергии и произведение давления на объем называют энтальпией.

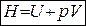, Дж (1.17)

III. Изотермический процесс

Рис. 1.5. Изотермический процесс в PV – диаграмме

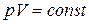
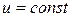
График – изотерма

Процесс 1-2 – изотермическое расширение газа;

Процесс 2-1 – изотермическое сжатие газа.

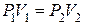
(1.18)

Отношение абсолютных давлений обратно пропорционально отношению объемов.

(1.19)

Вся теплота, подведенная к газу в изотермическом процессе, расходуется на совершение механической работы.

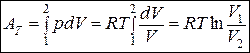(1.20)

т.к.

IV. Адиабатный процесс.

Процесс, осуществляющийся без подвода и отвода теплоты, т.е. dq=0, q=0.

Практически адиабатный процесс происходит при расширении или сжатии газа в цилиндре и протекающий настолько быстро, что теплообмен с окружающей средой не успевает произойти.

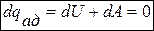
(1.21)

Следовательно, работа в процессе адиабатного расширения осуществляется за счет изменения внутренней энергии рабочего тела.

(1.22)

Уравнение адиабаты

(1.23)

где 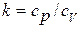- показатель адиабаты

График – адиабата – неравнобокая гипербола, более крутая, чем изотерма.

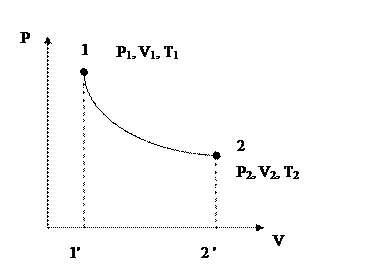
Рис. 1.6. Адиабатный процесс в PV – диаграмме.

V. Политропный процесс.

В политропных процессах происходит изменение всех параметров.

Уравнение политропных процессов:

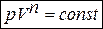
n – постоянная для данного процесса величина – показатель политропы с значением от 0 до ± .

Все рассмотренные термодинамические процессы являются частными случаями политропных процессов:

n=0, 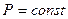изобарный процесс

n=1, изотермический процесс

n=k, 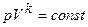адиабатный процесс

n=± , 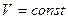изохорный процесс

Для политропного процесса:

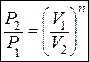, , (1.24)

(1.25)

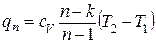
1.5. Второй закон термодинамики. Цикл Карно.

Циклом называется последовательность определенных термодинамических процессов, в которых рабочее тело, протерпев ряд изменений, возвращается в первоначальное состояние.

В основу расчета тепловых двигателей положены идеальные круговые процессы, циклы. Процесс подвода теплоты в идеальных циклах рассматривается без изменения химического состава рабочего тела. В реальных циклах процесс подвода теплоты происходит в процессе сжигания топлива и рабочим телом в двигателях внутреннего сгорания являются продукты, образующиеся при горении.

Процесс отвода теплоты в идеальных циклах предусматривает наличие холодильника. В реальных циклах этот процесс осуществляется выпуском отработавшего рабочего тела в атмосферу. Процессы расширения и сжатия в реальных циклах сопровождаются теплообменом и не могут точно соответствовать адиабатным.

а) б)

Рис. 1.7. Круговой цикл в РV – диаграмме

На круговом цикле (рис. 1.7, а) на участке 1 – а – 2 к рабочему телу подводится теплота q₁, рабочее тело расширяется и производит работу, равную площади 1 – а – 2 – 3 – 4 – 1.

На участке 2 – б – 1 от рабочего тела отводится теплота q₂ (или выпускаются отработанные газы), а также рабочее тело сжимается, на что затрачивается отрицательная работа внешних сил соответствующая площади 2 – б – 1 – 4 – 3 – 2. В т. 1 цикл завершается и рабочее тело приобретает первоначальные параметры. Следовательно, внутренняя энергия рабочего тела не изменятся ().

На основании 1 – го закона термодинамики для цикла имеем:

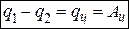(1.26)

А_ц – произведенная полезная работа.

Рассмотренный цикл называется прямым. По прямым циклам работают все тепловые двигатели.

Для непрерывной работы двигателя, превращающего теплоту в механическую энергию, необходимо иметь источник теплоты с высокой температурой Т₁ и сток теплоты (холодильник) с низкой температурой Т₂. При этом всегда желательно, чтобы в работу превратилась как можно большая доля подведенной теплоты.

Термический КПД цикла:

(1.27)

Термический КПД цикла – это отношение количества теплоты, превращенной в полезную работу, к количеству подведенной теплоты.

Рассмотрим цикл, осуществляющийся в обратном направлении, т.е. против часовой стрелки. Здесь линия сжатия расположена выше линии расширения, т.е. работа осуществляется на сжатие. Такой цикл называется обратным.

Положительная работа 1 – а – 2 – 3 – 4 меньше отрицательной 2 – б – 1 – 4 – 3, поэтому полезная работа не производится, а затрачивается работа от внешнего источника энергии. Теплота q₂ передается рабочему телу от холодного источника, а теплота q₁ отдается горячему источнику. В обратном цикле передача тепловой энергии происходит от холодного тела к горячему, при этом затрачивается работа, которая превращается в тепловую энергию.

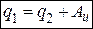(1.28)

Обратные циклы осуществляются в холодильных установках и тепловых насосах. Эффективность их работы оценивается холодильным коэффициентом:

(1.29)

Холодильный коэффициент – это отношение количества теплоты (тепловой энергии), переданное от холодного тела к количеству тепловой энергии, эквивалентной затраченной работе цикла А_ц.

В результате анализа множества циклов французский ученый Сади Карно нашел цикл с максимальным значением КПД.

Рис. 1.8. Перемещение поршня и изменение параметров рабочего тела в цикле Карно.

т. 1 – начало цикла: р₁, V₁, T₁

1-2 – изотермическое расширение рабочего тела при температуре Т₁ с подводом тепловой энергии q₁ и работой изотермического расширения 1 – 2 – 6 – 8 – 1.

2-3 – подвода теплоты нет, расширение по адиабате 2-3 до крайнего правого положения поршня 3. Работа адиабатного расширения 2 – 3 – 5 – 6 – 2.

3-4 – процесс сжатия рабочего тела при температуре Т₂ – изотермический процесс – с отводом теплоты q₂ и работой 3 – 4 – 7 – 5 – 3.

4-1 – процесс сжатия без отвода теплоты по адиабате 4-1, работа сжатия 4 – 1 – 8 – 7 – 4.

Таким образом, полезная работа определяется площадью 1 – 2 – 3 – 4 – 1 как разность площадей 1 – 2 – 3 – 5 – 8 – 1 и 3 – 4 – 1 – 8 – 5 – 3.

Термический КПД цикла Карно определяется по выражению:

(1.30)

В цикле Карно принято равенство отношений удельных объемов

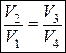(1.31)

С учетом последнего выражения

(1.32)

Из формулы (1.32) следует:

1. Термический КПД цикла Карно не зависит от свойств рабочего тела, а определяется только значением температур Т₁ и Т₂.
2. Термический КПД возрастает с увеличением Т₁ и уменьшением Т₂.
3. Термический КПД цикла Карно меньше единицы и может достигать 0,7 – 0,8.

Единице термический КПД цикла Карно мог бы быть равен при Т₂=0 или Т₁=∞,

что неосуществимо.

Реально создать двигатель, работающий по циклу Карно невозможно, т.к. процессы изотермического подвода и отвода тепловой энергии, а также адиабатного расширения и сжатия практически неосуществимы.

Цикл Карно является эталоном с максимальным КПД превращения тепловой энергии в работу. Реальный тепловой двигатель тем совершеннее, чем ближе его КПД к КПД цикла Карно, протекающего при тех же температурах.

Обратный цикл Карно также является эталоном для работы холодильных установок.

Холодильный коэффициент цикла Карно:

(1.33)

Дата добавления: 2015-07-25