
Читайте также:
|
| x = (-1)k arcsin а+pk |
Общая формула решения уравнения sin x= а имеет вид:
т.е. любое простейшее уравнение с синусом решается по этой общей формуле.
(-1)k - это знак «+» или «-» перед arcsin а, а вот почему «+pk», а не «+2pk»?
Докажем эту формулу:
1) Пусть показатель степени при (-1) k=2n – четный, т.е. [(-1)k =1], подставляем в общую формулу решения и получаем первое решение уравнения, т.е. х1= arcsin а+2pn
2) Пусть теперь аналогично k=2n+1- нечетный, т.е. [(-1)k=-1], подставляем в общую формулу решения и получаем второе решение уравнения
х2= - arcsin а+(2n+1)p =- arcsin а+2pn+p =p - arcsin а+2pn
Рассмотрим несколько примеров решения простейшего тригонометрического уравнения sinx= а
 1)sin x=
1)sin x= 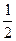 2) sin (2х +
2) sin (2х + 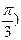 =
= 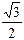 ;
;
х =(-1)k arcsin 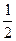 +pk 2х +
+pk 2х + 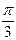 =(-1)k arcsin
=(-1)k arcsin 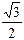 +
+ 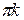 ;
;
х =(-1)k 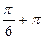 k решение ур-я 2х+
k решение ур-я 2х+ 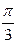 =(-1)k
=(-1)k 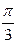 +
+ 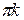 ;
;
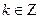 2х = (-1)k
2х = (-1)k 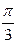 -
- 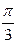 +
+ 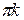 - делим почленно все уравнение на 2
- делим почленно все уравнение на 2
х =(-1)k 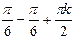 решение ур-я
решение ур-я 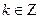
Учитывая свойства функции арксинус arcsin (-a) = - arcsin а, уравнение вида sin x=- а имеет решение
х = (-1)k(- arcsin a) + 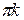 = (-1)k(-1)arcsin a +
= (-1)k(-1)arcsin a + 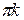 = (-1)k+1arcsin a +
= (-1)k+1arcsin a + 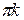
Итак, если sin x = - а, то общее решение имеет вид: х = = (-1)k+1 arcsin a + 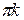
3) sin 2x = 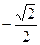
 2х = (-1)k+1 arcsin
2х = (-1)k+1 arcsin 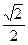 +
+ 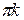 (в этой строке
(в этой строке 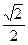 берем уже без знака «-»)
берем уже без знака «-»)
2х = (-1)k+1 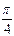 +
+ 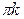 - делим почленно на 2
- делим почленно на 2
х = (-1)k+1 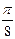 +
+ 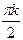 решение ур-я
решение ур-я 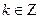
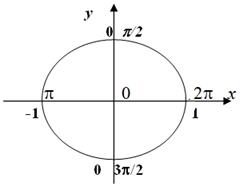
Существуют частные случаи решения простейших тригонометрических уравнений, когда не нужно пользоваться общей формулой решений, т.е. когда уравнение приравнивается к 0, -1 или 1. Для этого покажем в каких углах функция синус принимает данные значения на единичном тригонометрическом круге
 ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ УРАВНЕНИЯ sinx =а. y
ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ УРАВНЕНИЯ sinx =а. y
 1 p/2
1 p/2
sin x = -1, при х = 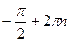 , , 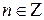
|
sin x = 0, при х =  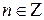
|
sin x = 1, при х = 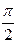 + 2pn, + 2pn, 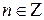
|
 p 0 2p x
p 0 2p x
0 0
P/2
4) sin 3x = -1 - частный случай; 3х = 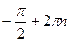 , х =
, х = 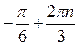 ,
, 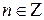 - ответ
- ответ
Аналогично рассматриваются выводы общих решений для уравнений вида
cos x =± а, tg x =± a, ctg x =± a
2. Рассмотрим уравнение cosx = а, уравнение имеет решение при | a | 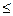 1.
1.
Аналогично, решая его графически, строим графики функций y=cos x и y= a






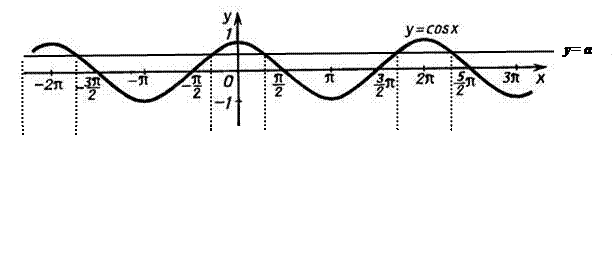
Учитывая периодичность, получаем два множества решений:
x1= arcos a + 2pn
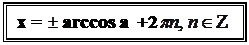 x2= - arcos a + 2pn
x2= - arcos a + 2pn
Т.о. общее решение уравнения cos x = а меет вид:
 Примеры:
Примеры:
1) cos x = 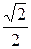 ; 2) 2 cos 3x – 1 = 0;
; 2) 2 cos 3x – 1 = 0;
х = 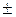 arсcos
arсcos 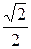 + 2
+ 2 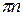 ; cos 3x = ½;
; cos 3x = ½;
х = 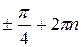 ,
, 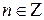 - решение уравнения 3x =
- решение уравнения 3x = 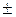 arcos ½ + 2pn;
arcos ½ + 2pn;
3x = 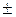 p/3 + 2pn – делим на 3 почл-но
p/3 + 2pn – делим на 3 почл-но
x = 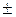 p/9 + 2pn/3,
p/9 + 2pn/3, 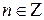 - ответ
- ответ
В силу свойств функции у = аrccos х (ни чет., ни нечетности), учитывая равенство
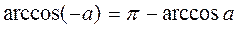 ,
,
уравнение cosx = - а имеет решение х =± (p - arccosa) +2πn
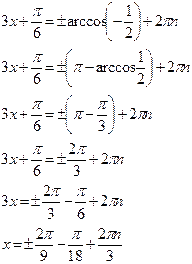
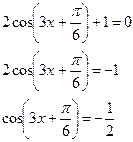 Пример 3:
Пример 3:
- ответ при 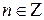
4) cos x = - 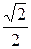 ; х =
; х = 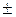 (π - arсcos
(π - arсcos 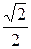 )+ 2
)+ 2 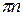 ; х =
; х = 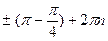 ; х =
; х = 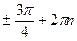 - решение уравнения
- решение уравнения 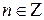
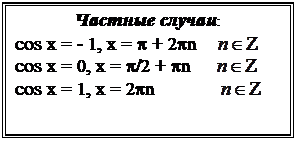
5) cos 4 x = - 1 – частный случай; 4x = p + 2pn; x = p/4 + 2pn/4;
x = 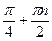 ,
, 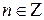 - ответ
- ответ
3.Уравнение: 
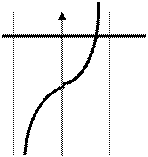 Учитывая, что все значения тангенсов углов находятся на линии тангенсов, (т.е. областью значений функции у = tg x является множество всех действительных чисел), данное уравнение будет иметь решения при любом а для хÎ(-p/2; p/2)
Учитывая, что все значения тангенсов углов находятся на линии тангенсов, (т.е. областью значений функции у = tg x является множество всех действительных чисел), данное уравнение будет иметь решения при любом а для хÎ(-p/2; p/2)

 y y
y y

 tgα
tgα
 a
a


 o x -p/2 0 p/2
o x -p/2 0 p/2
tgα tgx arctg a
T
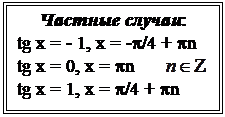
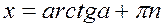 - одно общее решение
- одно общее решение 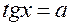
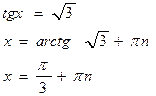 Пример 1:
Пример 1:
ответ при 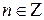
 В силу свойства нечетности: arctg(-a)=-arctga
В силу свойства нечетности: arctg(-a)=-arctga
|
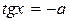 имеет решение вида:
имеет решение вида:
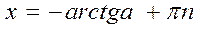 .
.
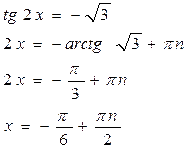
Пример 2:
| |||||
ответ при 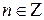
Пример 3: tg3x=0– частный случай; 3x = pn, х= 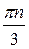 при
при 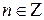 - ответ
- ответ
4.Уравнение: 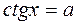 можно свести к уравнению
можно свести к уравнению 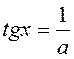
Учитывая свойства функции 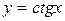 , её область определения хÎ(-p; p), область значений функции у = сtg x является множество всех действительных чисел, данное уравнение будет иметь решения при любом а
, её область определения хÎ(-p; p), область значений функции у = сtg x является множество всех действительных чисел, данное уравнение будет иметь решения при любом а
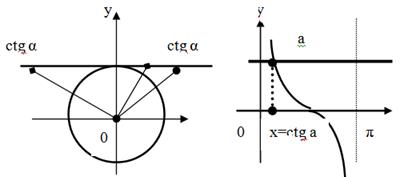
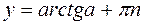 - общее решение
- общее решение 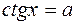
Пример 1:
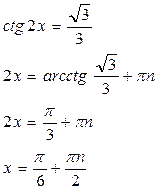
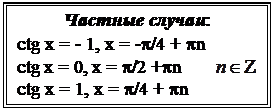
- ответ при 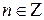
Пример 2:
ctg 3x = 1; 3x=p/4 + pn; x=p/12 + pn/3, 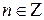 - ответ
- ответ
Учитывая, что 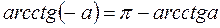 , уравнение
, уравнение
|
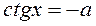 имеет решение вида:
имеет решение вида:
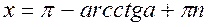
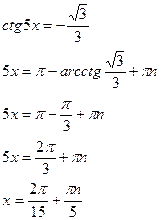
- ответ при 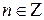
Загальні висновки:
Для розв'язання найпростіших тригонометричних рівнянь використовуються формули їх загальних рішень та окремі випадки, подані у наступній таблиці:
Эта таблица должна быть написана в конспекте обязательно!!!
| Уравнение | Общее решение | Частные случаи | Приложения |
|
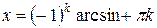
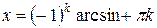
| 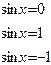  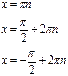 
|
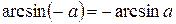 | a |
| a |  1. 1.
|
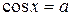
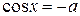
| 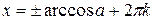
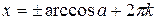
| 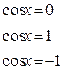 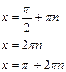
|
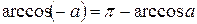 | a |
| a | 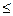 1. 1.
|
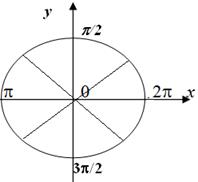
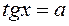 tg = - a
tg = - a
| 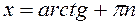 x = - arctg a +pn
x = - arctg a +pn
|
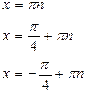 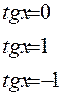
|
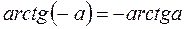 a Î R.
a Î R.
|
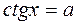 ctg = - a
ctg = - a
| 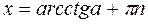 x = p - arctg a +pn
x = p - arctg a +pn
| 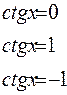 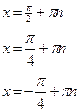
|
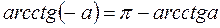 a Î R.
a Î R.
|
Практическая работа по простейшим уравнениям:
Решение уравнений:
Дата добавления: 2015-07-25; просмотров: 158 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение, в котором неизвестное (переменная) находится под знаком тригонометрической функции, называется тригонометрическим. | | | Вопрос 109 |