Уравнение, в котором неизвестное (переменная) находится под знаком тригонометрической функции, называется тригонометрическим.

Например: sin 2x = 1; 2 cos x + = sin x; sin²x + 2 cos x + cos 3x = 0.

При нахождении функций, обратных к у = sin x, (у = cos x и т.д.), мы решая уравнение

у=sinx, (у=cos x) относительно х, находили число (угол, дугу) х = arcsin у (или переименовав обозначения на традиционные, получали у =arcsin х –функцию, обратную данной)

Пример: sin x = a; х = arcsin a, х – угол (дуга), синус которого равен a.

sin x = 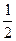; х = arc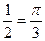sin ; sin .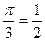

ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ.

1. Рассмотрим уравнение

sin x= а

при | a | >1 – решений нет. След-но, уравнение имеет решение при | a | 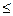1.

Решаем данное уравнение графически, построив в одной системе координат графики у=а и у=sin x. Точки пересечения этих графиков дадут решения, которые будут в силу периодичности тригонометрических функций повторяться.

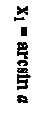
Получили два множества решений:

(1) х₁= arcsin а +2pn

(2) х₂=p - arcsin а +2pn

Дата добавления: 2015-07-25