Читайте также:
|
Одним із способів усунення корелювання пояснюючої змінної з випадковим відхиленням є метод інструментальних змінних.
Сутність цього методу полягає в заміні змінної, що корелює із залишками, інструментальною змінною (ІЗ), яка повинна мати такі властивості:
· корелювати (бажано значною мірою) із заміненою пояснюючою змінною;
· не корелювати з випадковим відхиленням.
Опишемо схему використання інструментальних змінних на прикладі парної регресії, в якій
Y = β0 + β1X + ε. (8.1)
Змінну X замінюють змінною Z такою, що cov(Z; X) ≠ 0 і cov(Z, ε) = 0. Принципи використання інструментальних змінних передбачають виконання
таких умов:
M (εt) = 0,cov(zt, εt). (8.2)
Відповідні вибіркові оцінки даних умов такі:
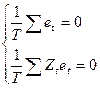. (8.3)
У розгорнутому вигляді остання система має вигляд:
. (8.4)
Звідки
. (8.5)
Нехай зі збільшенням обсягу вибірки D(X) прямує до деякої скінченної межі 
, коваріація cov (Z, X), до скінченної межі 
.
Покажемо, що в цьому разі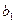 
прямує до істинного значення 
. З останньої системи маємо:
Тут ми скористались такими співвідношеннями: 
, тому що 
При великих обсягах вибірки розподіл 
прямує до нормального:
де
(8.6)
.
Дата добавления: 2015-07-25; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оцінювання параметрів економетричних моделей у разі наявності автокореляції залишків | | | Поняття лага та лагових моделей в економіці |