Оцінювання параметрів економетричних моделей у разі наявності автокореляції залишків

Для оцінювання параметрів економетричних моделей з автокорельованими залишками в основному використовуються наступні методи:

1) метод Ейткена (УМНК);

2) метод перетворення вихідної інформації;

3) метод Кочрена – Оркатта;

4) метод Дарбіна.

Перші два методи використовують у випадку, коли залишки задовольняють авторегресійній схемі першого порядку, третій і четвертий - можна застосовувати тоді, коли залишки описуються за авторегресійною схемою вищого порядку.

Розглянемо докладніше метод Ейткена (узагальнений метод найменших квадратів). Цей метод (як і у випадку гетероскедастичності) базується на перетворенні вихідної моделі з урахуванням коваріації залишків (дисперсійно-коваріаційної матриці залишків) у модель без корельованих залишків, до якої потім застосовується метод найменших квадратів.

Нехай в економетричній моделі 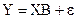випадкова величина задовольняє авторегресійній схемі першого порядку , де u_i – нормально розподілені залишки. Тоді оператор оцінювання параметрів моделі, як і у випадку гетероскедастичності, буде мати вигляд:

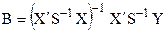, (7.9)

де матриця S має вигляд:

. (7.10)

Параметр ρ наближено можна визначити на основі залишків вибіркової моделі, оціненої за звичайним методом найменших квадратів. З цією метою розраховують так званий скоригований циклічнийкоефіцієнткореляції:

. (7.11)

Тоді параметри ρ дорівнюють:

. (7.12)

Оскільки коваріація залишків у матриці S при α >2 часто наближається до нуля, у практичних розрахунках зразу ж можна визначити матрицю S^-1, обернену до матриці S:

. (7.13)

Використання виразу (7.13) значно полегшує і прискорює розрахунки оцінок параметрів моделі.

Найкращий незміщений лінійний точковий прогноз у випадку автокореляції залишків обчислюється за наступною залежністю:

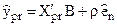, (7.14)

де B – вектор оцінок параметрів моделі, отриманих узагальненим методом найменших квадратів (УМНК); ρ – параметр з матриці S; - залишок в останньому спостережені, обчислений для моделі, параметри якої оцінені на основі узагальненого методу найменших квадратів; 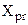- вектор прогнозних значень пояснюючих змінних моделі.

Інтервальні прогнози у випадку автокореляції залишків обчислюють за такими ж самими залежностями, як і у випадку гетероскедастичності.

Дата добавления: 2015-07-25