бесконечно удаленной точке.

Очевидно, что z = ¥ для любой аналитической функции является особой, а изолированной особой, если существует окрестность бесконечно удаленной точки, где кроме нее нет других особых точек (существует такое число 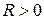, что для любых 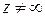таких, что 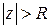, функция является аналитической).

Для характеристики особенности в бесконечно удаленной точке функции 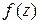сделаем замену: 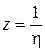. Тогда 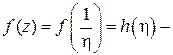аналитическая функция в области кроме точки .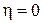

Изолированная особая точка 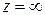называется устранимой, плюсом или существенно особой для функции 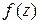тогда и только тогда, когда таковой является точка 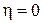для функции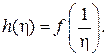

Таким образом, исследование особенности на бесконечности сведено к исследованию для конечной особой точки. Рассмотрим, какой вид имеет ряд Лорана в окрестности бесконечно удаленной точки.

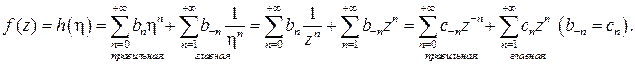
(40)

Если 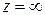– устранимая особая точка, то в ряду Лорана отсутствует главная часть, следовательно, 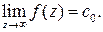В этом случае принято считать, что в бесконечности у функции особенности нет.

Вычет в бесконечно удаленной точке определяется равенством:

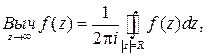(41)

если контур ориентирован по часовой стрелке и для всех конечных 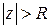функция аналитична.

В силу ориентации контура (он является границей окрестности бесконечно удаленной точки) имеем

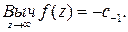(42)

Отметим, что в случае устранимой особенности в точке 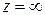, вычет не всегда равен нулю (сравните с конечной устранимой особой точкой), т. к. коэффициент 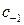в ряду Лорана в окрестности 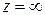находится в правильной части (см. (40)).

Основные способы вычисления вычета в бесконечно удаленной точке:

1) непосредственно по определению (см.(41));

2) разложение в ряд Лорана и использование равенство (42);

3) использование следствия из основной теоремы о вычетах, которое мы сформулируем в виде теоремы.

Теорема: Если функция 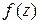аналитична во всей комплексной плоскости, кроме конечного числа изолированных особых точек: С₁, С₂, …, С_N (C_k ¹ ¥, k=1,2,…,N), то сумма всех вычетов, включая вычет в бесконечно удаленной точке равна нулю, т. е.

(43)

Из равенства (43) получаем:

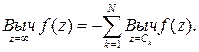(44)

Пример: Найти вычет точке 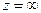следующих функций

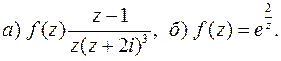
В силу равенства (44) и результатов предыдущего примера получаем: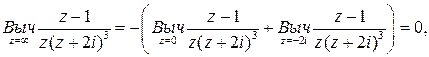

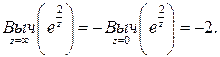
Дата добавления: 2015-07-20