Вычеты функции

Определение:Вычетом аналитической функции f(z) в конечной изолированной особой точке z₀ (z₀ ¹µ) называется комплексное число

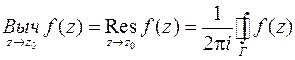(34)

при условии, что Г – положительно ориентированный кусочно-гладкий замкнутый контур, содержащий внутри себя единственную изолированную особую точку z₀ .

Равенство (33) показывает, что вычет равен коэффициенту перед в ряду Лорана (31) данной функции в окрестности точки z₀ , т.е.

(35) Равенство (35) дает один из способов вычисления вычета – разложение в ряд Лорана (31) и нахождение коэффициента с_–1. Этот способ достаточно трудоемкий, но он оказывается практически единственным в том случае, когда z₀ – существенно особая точка. В других случаях есть более простые способы нахождения вычета. Если z₀ – устранимая особая точка, то ряд Лорана (31) по определению не имеет главной части, т.е. все коэффициенты

Рассмотрим случай, когда z₀ – полюс порядка m =1 (простой полюс). Ряд Лорана (31) принимает вид Следовательно,

(36)

В случае, когда , т.е. z₀ – полюса первого порядка, иногда удобнее использовать формулу

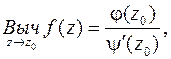(37)

(она является следствием формулы (36)).

Если z₀ – полюс порядка m >1, то

(38)

Пример. Вычислить вычеты функции во всех конечных изолированных особых точках:

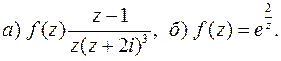
Решение: Особыми точками функции являются Прежде, чем находить вычеты в этих точках, нужно выяснить характер особенности, т. к. от этого зависит способ (выбор формулы) вычисления. Для определения характера особенности найдем: 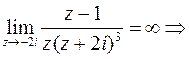эти точки являются полюсами, но разного порядка. Для функции 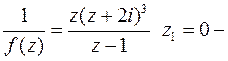нуль 1-го порядка, а 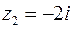– нуль 3-го порядка (см. степени соответствующих сомножителей). Значит, 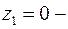полюс 1-го порядка, а 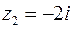– полюс 3-го порядка. Находим вычеты:

Для функции особой является точка , причем, это существенно особая точка, т. к. не существует. Действительно, при стремлении к нулю по действительной оси (при 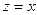) односторонние пределы не совпадают: Воспользуемся равенством (35), для этого разложим функцию в ряд Лорана в окрестности нуля и найдем коэффициент :

Основная теорема о вычетах: (Коши) Пусть аналитическая функция в области D, кроме конечного числа изолированных особых точек: С₁, С₂, …, С_N (C_k ¹ ¥, k=1,2,…,N). Тогда справедлива формула

(39)

где – кусочно-гладкий контур в области D, содержащий внутри себя точки: С₁, С₂, …, С_N.

Данная теорема позволяет вычислять контурные интегралы с помощью вычетов.

Пример. Вычислить

Особыми точками подынтегральной функции являются точки они находятся внутри контура , т. к. он представляет собой окружность радиуса 3 с центом в точке По формуле (39) получаем: 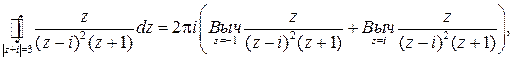т.к. простой полюс, а – полюс 2-го порядка, то используем формулы (36) и (38):

Дата добавления: 2015-07-20