
Читайте также:
|
Для подготовки к занятию дома
1. Подготовьтесь к контрольной работе, используя теоретические задания для развития и контроля владения компетенциями.
2. Просмотрите решенные ранее задания по разделам «Ряды», «Функции нескольких переменных», обратите особое внимание на разобранные примеры решения типовых задач.
3. Повторите таблицу основных производных.
4. Вспомните правила дифференцирования функции нескольких переменных.
5. Повторите способы отыскания радиуса сходимости степенного ряда.
6. Вспомните формулы для нахождения коэффициентов ряда Фурье.
7. Изучите еще раз выполненные задания индивидуальных домашних работ, обратите внимание на сделанные замечания преподавателя при их проверке и сделайте работу над ошибками.
8. Прорешайте примерный вариант контрольной работы, приведенный ниже.
На занятии по указанию преподавателя решите предложенный Вам вариант контрольной работы.
Дома подготовьтесь к очередному занятию по следующему разделу.
Рекомендуемая литература
[1] главы 10 - 12.
[2] часть 1, глава VIII; часть 2, глава I; III §§ 1-4; 8.
[3] главы 5; 8.
[6] главы 12 - 14.
[7] главы XII - XIV.
Теоретические задания
Для развития и контроля владения компетенциями
Вопросы для подготовки к контрольной работе
1. Числовые ряды: основные понятия, необходимые условия сходимости ряда. Остаток ряда.
2. Ряды с положительными членами и признаки их сходимости: признаки сравнения, Даламбера, Коши (радикальный и интегральный).
3. Знакочередующиеся ряды, признак Лейбница.
4. Степенные ряды и область их сходимости.
5. Разложение функций в степенной ряд. Разложение некоторых элементарных функций ( ,
,  ,
,  ,
,  ,
, 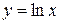 ,
, 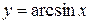 ,
,  ) в ряд Тейлора (Маклорена).
) в ряд Тейлора (Маклорена).
6. Применение степенных рядов к приближенным вычислениям значений функций, интегралов, пределов.
7. Системы ортогональных функций. Примеры.
8. Тригонометрические ряды и их сходимость. Ряды Фурье. Формулы для вычисления коэффициентов ряда Фурье.
9. Ряды Фурье для четных и нечетных периодических функций.
10. Функции нескольких переменных, основные определения (область определения, область значения, график функции двух переменных, линии и поверхности уровня).
11. Частные производные первого и более высоких порядков.
12. Экстремум функции двух переменных: определение, необходимое и достаточное условия экстремума.
13. Условный экстремум. Метод множителей Лагранжа.
14. Полный дифференциал и его приложение к приближенным вычислениям.
Дата добавления: 2015-07-25; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Практическое занятие № 48 | | | Практические задания |