
Читайте также:
|
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Пусть функция y = f(x) дифференцируема в  -окрестности точки
-окрестности точки  , а в самой точке
, а в самой точке  непрерывна. Тогда
непрерывна. Тогда
· если  при
при 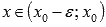 и
и  при
при 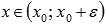 , то
, то  - точка максимума;
- точка максимума;
· если  при
при 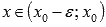 и
и  при
при 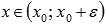 , то
, то  - точка минимума.
- точка минимума.
Другими словами:
· если в точке  функция непрерывна и в ней производная меняет знак с плюса на минус, то
функция непрерывна и в ней производная меняет знак с плюса на минус, то  - точка максимума;
- точка максимума;
· если в точке  функция непрерывна и в ней производная меняет знак с минуса на плюс, то
функция непрерывна и в ней производная меняет знак с минуса на плюс, то  - точка минимума.
- точка минимума.
Дата добавления: 2015-07-25; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Достаточные признаки возрастания и убывания функции. | | | Алгоритм. |