
Читайте также:
|
Карты алгебры логики представляют собой табличное изображение всех возможных событий. Рассмотрим представление на карте двух событий A и B.
Карта событий A и B может быть представлена в двух видах (рис. 2.27а и рис. 2.27б).
| A 0 | ||
| B |  A не появляется
и
B не появляется
A не появляется
и
B не появляется
|  A появляется
и
B не появляется
A появляется
и
B не появляется
|
 A не появляется
и
B появляется
A не появляется
и
B появляется
| 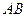 A появляется
и
B появляется
A появляется
и
B появляется
|
а
| AB | |||
б
Рис. 2.27. Варианты карт для событий A и B
Пример 2.11.1. Представить на карте функцию T = A + B.
Согласно правилу IV таблицы 2.13  . Для полного представления события A необходимо учесть как член AB, так и член
. Для полного представления события A необходимо учесть как член AB, так и член  .
.
|
|
|
|
|
|
Рис. 2.28. Карта функций T=A+B
Представим функции T=A, T=B и T=A+B в виде таблиц (рис.2.28). Функция T=A+B представлена на нижней карте.
Карты двух переменных легко обобщаются на случай трёх и четырёх переменных. Каждый раз при появлении новой переменной число ячеек удваивается. Если карта двух переменных состояла из четырёх ячеек, то карта трёх переменных будет состоять из восьми ячеек (рис. 2.29), а карта четырёх переменных из 16 ячеек (рис.2.30). Другими словами, число ячеек равно 2 n, где n – число переменных.
| AB | |||||
| C | T=A+BC | ||||
| 1,2 | 1 2 |
Рис. 2.29. Карта событий для трёх переменных
| AB | ||||
| CD | 1,2 | |||
| 1,2 | ||||
| 1,3 | 1,3 | |||

|
Рис. 2.30. Карта событий для четырёх переменных
Правила отображения логических функций на картах состоят в следующем:
Шаг 1. Представляем функцию в виде суммы произведений;
Шаг 2. Выбираем поочерёдно произведения и вписываем единицы в ячейки карты, соответствующие каждому произведению.
Для каждого из произведений рассматриваются входящие в него переменные. Если переменная входит без отрицания, то она может попасть в таблицу функции. Однако в таблицу попадут лишь те из них, на которые не влияют ограничения, накладываемые другими произведениями.
Пример 2.11.2. Рассмотрим функцию T=A+BC, образованную слагаемыми A и BC. Слагаемое A входит без отрицания и вносится в карту. Это слагаемое не зависит от других переменных, которые должны быть представлены на карте всеми значениями. Это показано символами 1 на рис. 2.29. Во втором члене BC переменная B также становится кандидатом на внесение в ячейки таблицы, но она уже связана с переменной C. Следовательно, только в тех ячейках B появятся единицы, для которых C не имеет отрицания. Это обозначено символом 2 в ячейках таблицы рис. 2.29.
Процедура для двух переменных выглядит довольно просто. При построении карты для четырёх и пяти переменных уже требуется соблюдение регулярных правил заполнения ячеек.
Пример 2.11.3. Рассмотрим функцию 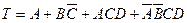 , приведенную на рис. 2.30.
, приведенную на рис. 2.30.
Единицы, принадлежащие A, попадут в ячейки, связанны с A, всех других переменных. Для отображения  отбираются сначала восемь ячеек, связанных с переменной A, а затем выделяют четыре из них, связанные с величиной C (обозначено на карте символом 2). Для третьего члена ABC сначала выделяют ячейки переменной A без отрицания, затем из них выбирают ячейки с переменной C и далее те из выбранных ячеек, которые содержат величину D, не имеющую отрицания. Четвёртый член
отбираются сначала восемь ячеек, связанных с переменной A, а затем выделяют четыре из них, связанные с величиной C (обозначено на карте символом 2). Для третьего члена ABC сначала выделяют ячейки переменной A без отрицания, затем из них выбирают ячейки с переменной C и далее те из выбранных ячеек, которые содержат величину D, не имеющую отрицания. Четвёртый член  займет ячейку на пересечении столбца
займет ячейку на пересечении столбца  – 00 со строкой CD – 11.
– 00 со строкой CD – 11.
Пример 2.11.4. Рассмотрим функцию произведения сумм T=(A+B)(C+D), которая часто встречается при анализе деревьев отказов.
Возможны два способа решения этой задачи.
Первый – предусматривает непосредственное построение карты по заданной функции, Для этого берутся все ячейки, соответствующие члену A+B, означающему все A или все B. Затем из них выделяются ячейки, соответствующие C+D, означающие все C или все D. Описанная процедура проиллюстрирована на рис. 2.31а.
| AB |  
| |||
| CD | ||||
 
| 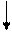
| |||
 а – T=(A+B)(C+D)
а – T=(A+B)(C+D)
Другой путь заключается в почленном логическом перемножении переменных и представлении функции в виде T=AC + AD + BC + BD.
Далее заполняется карта, как показано на рис. 2.31б.
Второй метод предпочтительнее из-за своей простоты и последовательности. (Решить задачу 3).
| AB | ||||
| CD | ||||
| 2,4 | ||||
| 2,4 | 1,2,3,4 | 1,2 | ||
| 1,3 |
б – T=AC + AD + BC + BD
1 2 3 4
Рис. 2.31. Карта функции T=(A+B)(C+D) и T=AC + AD + BC + BD
Дата добавления: 2015-07-25; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аппарат логического анализа | | | Упрощение выражений с помощью карт |