
Читайте также:
|
Цель этого раздела состоит в изложении процедуры анализа логической структуры процессов. Методология такого анализа основана на понятиях булевой алгебры или алгебры логики (Arnold, Bradford H., 1962).
В алгебре логики переменные, обозначаемые заглавными буквами, имеют, как правило, смысл некоторых событий или фактов. Например, можно обозначить символом A событие, состоящее в повреждении некоторой детали машины. Если это происходит, то мы говорим, что A = T или что A истинно. Если событие не происходит, говорим, что – A=F или что A ложно. Для удобства в алгебре логики принято обозначать символом 1 истину (появление) и символом 0 ложь (непоявление). Вообще говоря, такие высказывания справедливы для некоторого определенного интервала времени и вероятности, связанной с появлением события.
Переменные в алгебре логики принимают два значения: истина или ложь (появление или непоявление). Аналогично и функции прини-
мают два значения в зависимости от комбинации логических переменных. Функции образуются с помощью операций И, ИЛИ и НЕ. Смысл этих операций определяется таблицами истинности 2.11, 2.12 и 2.13 соответственно.
Истинностное значение функции задается значениями переменных, входящих в неё. Например, пусть функция A имеет вид
 .
.
Чтобы определить истинное значение A, надо знать истинностные значения четырёх переменных.
Вычисление значения отдельных членов ведется в следующем порядке: 1 – НЕ, 2 – И и 3 – ИЛИ.
Таким образом, если B = ЛОЖЬ, С = ИСТИНА, D = ИСТИНА и E = ЛОЖЬ, то, используя таблицы 2.10, 2.11 и 2.12 получим
 .
.
| Таблица 2.11 | Таблица 2.12 | Таблица 2.13 | ||
| Оператор И | Оператор ИЛИ | Оператор НЕ |
| X | Y | XY | X | Y | X+Y | X |  (не X)
(не X)
| ||
| T | T | T | T | T | T | T | F | ||
| T | F | F | T | F | T | F | T | ||
| F | T | F | F | T | T | ||||
| F | F | F | F | F | F |
*T – ИСТИНА (появление), F – ЛОЖЬ (непоявление).
Порядок выполнения операций может быть изменен применением скобок, причём выражения внутренних скобок вычисляются первыми.
Например,

При некотором навыке записывать каждый шаг необязательно.
Поскольку таких значений всего два, то нетрудно перебрать все возможные варианты и доказать справедливость каждого выражения с помощью правил выполнения операций, приведённых в табл. 2.11, 2.12 и 2.13.
Пусть, например, X, Y и Z – некоторые три логические переменные. Правила упрощения выражений, приведённые для этого случая в табл. 2.14 могут быть легко получены подстановкой всех возможных значений переменных.
Таблица 2.14
Правила упрощения логических выражений
| I | 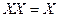
| 
|
| II | 
| 
|
| III | 
| 
|
| IV | 
| 
|
| V | 
| 
|
| VI | 
| 
|
Преобразование сложных логических выражений с помощью основных правил, приведённых в разделе 2.11.1, становится весьма трудоёмким процессом. Когда число переменных не превышает шести, широко применяется и дает хорошие результаты метод карт.
Дата добавления: 2015-07-25; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| При помощи таблиц решений | | | Методом карт |