Лабораторная работа № 4

Расчет характеристик моделей массового обслуживания.

Марковский процесс типа “гибель и размножение”может быть использован в качестве модели большого количества реальных процессов для анализа их показателей эффективности функционирования. В предельном стационарном режиме такой процесс характеризуется вероятностями состояний, которые определяются по формулам:

При этом граф состояний процесса имеет вид:

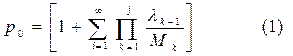
Здесь λj, Μj –интенсивности переходов для ј-го состояния. Существует несколько типовых систем массового обслуживания,описываемых процессами ”гибель и размножение”, для которых общие выражения (1),(2) конкретизируются.

1. Системы без потерь с неограниченным ожиданием и источником с бесконечным числом требований.

Предпологается,что система содержит N одинаковых обслуживающих каналов с одинаковой интенсивностью обслуживания

j – число требований в системе;

λj = λ

На основе формул (1),(2) получаем выражения для расчета вероятностей состояний:

Существование конечной средней очереди в системе возможно при выполнении условия:

В этом случае показатели эффективности системы расчитываются по формулам:

1.Вероятность простоя системы –P₀.

2.Среднее число требований в очереди

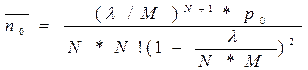
3.Среднее число занятых каналов

4.Среднее число требований в системе (6)

5.Среднее время ожидания требования в очереди

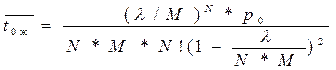
6. Среднее время пребывания требования в системе

2. Системы без потерь с конечным числом требований.

В подобных системах интенсивность потока поступающих требований зависит от состояния системы, поскольку общее число требований в системе остается постоянным.

Считаем, что система имеет N каналов с интенсивностью обслуживания М для каждого канала и источник, содержащий постоянное число m требований, поступающих с интенсивностью λ для каждого требования, причем m>N.

Граф состояний системы имеет вид:

Интенсивность переходов в графе определяется следующим образом:

0 £ j £ m-1

С учетом выражений для λj, Мj на основе (1),(2) получаются формулы для расчета вероятностей состояний:

Показатели эффективности системы расчитываются по формулам:

1.Вероятность простоя системы –Р₀.

2.Среднее число требований в очереди

3. Среднее число занятых каналов:

4. Среднее число требований в системе:

(9)

5. Среднее время ожидания требования в очереди:

6. Среднее время пребывания требования в системе:

Пример 1. На дробильно-перегрузочный комплекс в среднем за 8 часов поступает 200самосвалов со щебнем. Комплекс включает 3 разгрузочных пункта. В среднем разгрузка самосвала занимает 4 минуты. Требуется определить основные характеристики этого объекта как системы массового обслуживания, если поток самосвалов можно считать простейшим, а время разгрузки имеет экспоненциальное распределение.

Данный объект может рассматриваться как система массового обслуживания без потерь и источником с бесконечным числом требований. Определим ее параметры.

Число каналов обслуживания равно трем (три разгрузочных пункта), т.е. N=3.

Интенсивность входного потока требований (поток самосвалов) час^-1

Интенсивность обслуживания одного канала:

час^-1=15 час^-1

Граф состояний системы:

l l l l l l

0 1 2 3...... j......

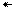m 2m 3m 3m 3m 3m

Поскольку условие (5) выполняется l<3m, то по формуле (3) вычисляем вероятность простоя системы :

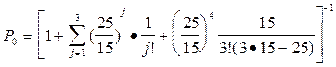
Затем по формулам (6) рассчитываются показатели эффективности системы.

Пример2. 6 Абонентов работают с двумя информационными центрами. В течении одного часа каждый абонент в среднем обращается с запросом на обслуживание 10 раз. Обслуживание одного абонента в среднем продолжается 3 минуты. Если оба центра на момент запроса заняты, то абонент переходит на режим ожидания. Определить показатели эффективности такого объекта как системы массового обслуживания, если поток запросов можно считать простейшим, а время обслуживания подчиняется экспоненциальному закону распределения.

Поскольку обслуживаемый или находящийся в режиме ожидания абонент послать новый запрос не может, а число абонентов конечно, то данный объект может рассматриваться как система без потерь с источником конечного числа требований. Определим ее параметры.

Число каналов обслуживания равно двум, т.е. N=2.

Постоянное число требований в системе равно шести, т.е. m=6.

Интенсивность одного требования (интенсивность потока заявок одного абонента) l=10ча .

Интенсивность обслуживания одного канала

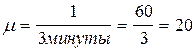час^-1

Граф состояний системы имеет вид:

6l 5l 4l 3l 2l l

0 1 2 3 4 5 6

m 2m 2m 2m 2m 2m

По формулам (9) рассчитываются показатели эффективности системы.

Задание1. На обогатительной фабрике участок КИП и А обслуживает А единиц оборудования. В среднем через В минут каждая единица оборудования требует обслуживания одним человеком в течении С минут. Определить минимально необходимое количество электрослесарей на участке, чтобы требующий обслуживания объект находился в этом состоянии в среднем не более Д минут?

А,В,С,Д - задаются преподавателем, причем Д>С.

Пределы варьирования:

Задание2. На базу материально-технического снабжения под погрузку поступает за восьчасовую смену в среднем А автомобилей. Один погрузчик грузит автомобиль в среднем В минут. Определить минимально необходимое количество погрузчиков для того, чтобы среднее число автомобилей в очереди под погрузку не превышало С штук.

А,В,С - задаются преподавателем. Пределы варьирования:

Дата добавления: 2015-07-25