Формулировка проблемы (постановка задачи).

Построение математической модели функционирования системы.

Составление алгоритма, программы, ее отладка на ЭВМ.

Планирование вычислительных экспериментов.

Проведение вычислительных экспериментов.

При имитации функционирования систем на ЭВМ построенная математическая модель преобразуется в моделирующий алгоритм, в котором сохраняются логическая структура, последовательность протекания процессов во времени, характер и состав информации о состоянии процессов.

ЭВМ представляют собой устройства дискретного типа, а потому и моделирующий алгоритм должен являться дискретной аппроксимацией построенной математической модели функционирования системы. Особенность имитации поведения исследуемой системы на ЭВМ сводится к определению правила развертывания квазипараллельных процессов функционирования множества элементов в системе в последовательный моделирующий алгоритм.

В настоящей работе применяется наиболее простой вариант решения данной задачи. Интервал времени [0;Т], в течении которого рассматривается работа системы, разбивается на интервалы длиной Dt, из-за чего данный способ решения получил название принципа Dt.

В пределах каждого интервала Dt последовательно вычисляются приращения всех значений переменных в модели, и производится соответствующее изменение состояния отдельных элементов модели. При достаточно малых Dt получается хорошее приближение имитируемых процессов к процессам в реальной системе с параллельным выполнением операций.

Обычно такой способ построения имитационных моделей используется при моделировании непрерывных динамических систем. Принцип Dt является наиболее универсальным принципом построения моделирующих алгоритмов, хотя и наименее экономичным с точки зрения вычислений на ЭВМ.

2. Методы имитации случайных факторов при моделировании систем.

Базовой последовательностью случайных чисел, используемой для формирования в ЭВМ элементов различной природы, с различными законами распределения, является совокупность случайных чисел с равномерным законом распределения на интервале [0;1]. Существует несколько способов получения таких чисел. Простейшим примером генератора случайных чисел является рекуррентное соотношение:

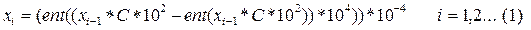
Здесь С – постоянное число 0<С<1 с четырьмя цифрами после запятой; Х0- число такого же формата(Х0 должно быть задано).

Пример С=0,2548

Х0=0,9351

Если имеется последовательность чисел х0, x1, x2,…..xi,…равномерно распределенных на интервале[0,1], то можно определить последовательность y0, y1, y2…yi,…,имеющую заданную плотность распределения f(y) из решения уравнения:

Пример. Получить последовательность чисел{yi},имеющих показательное распределение:

В соответствии с (2)имеем:

В некоторых случаях уравнение(2) аналитически решить трудно. В этом случае либо применяются численные методы его решения, либо эмпирические формулы. Например, величина u будет иметь нормальное распределение с параметрами m_u =0_; s_n=1

Обычно достаточно принять .

Для получения нормальной последовательности с параметрами m_y=a; s_y=s достаточно выполнить линейное преобразование:

y=su+a (4)

Определение объема вычислительных экспериментов. Допустим необходимо определить число экспериментов N для оценки некоторого показателя эффективности E, являющегося функцией параметров системы, алгоритма или структуры. Для этого пользуются формулой:

где 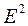– точность оценки; – аргумент нормального закона распределения, соответствующий заданной доверительной вероятности 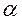и определяемый по таблицам Лапласа, т.е.

Обычно среднее квадратичное отклонение S_E неизвестно.

Поэтому предварительно проводится серия вычислительных экспериментов, в ходе которых оценивается S_E, а затем вычисляется необходимый объем эксперимента по (5).

Методика расчета последующих состояний типовых динамических звеньев.

Интегрирующее звено:

X W(p) Y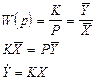

С учетом дискретного характера времени, производную представим в виде отношения приращений:

Перед началом расчетов Y(0) должно быть задано.

2. Дифференцирующее звено:

Перед началом расчетов X(0) должно быть задано.

3.Аппериодическое звено:

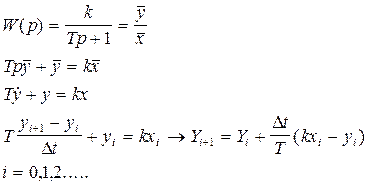
Перед началом расчетов Y(0) должно быть задано.

Пример. Дана система автоматического управления в виде структурной схемы рис.1 Здесь обозначено:

Х F

Н.Э Х- вход системы;

У- выход системы

F- возмущающее воздействие

Н.Э.-нелинейный элемент

P

y

Исходные данные:

Значения параметров структурной схемы:

Т₁=2; Т₂=1; Т₃=0,5; К₁=0,5; К₂=2

Зависимость выхода нелинейного элемента от входа:

Х_вых=Х²_вх

Закон изменения входной переменной:

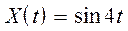
4.Шаг квантования независимой переменной t по времени при машинной имитации:

5.Закон распределения случайной величины F: F распределена по нормальному закону с математическим ожиданием 0,4 и средним квадратическим отклонением 0,3.

6.Начальные состояния инерционных звеньев: все выходы инерционных звеньев в момент t=0 равны нулю.

Требуется методом рассчитать процесс изменения выхода системы у(t) на интервале Т=3

Вначале преобразуем структурную схему системы и введем промежуточные переменные (рис.2):

F

Н.Э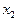

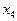
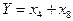
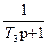
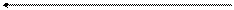
Рис.2.

Основные соотношения между переменными имеют вид:

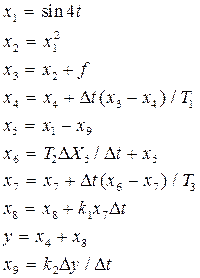
Для определения количества расчетных точек заданный временной интервал 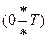разделим на шаг квантования по времени :

Порядок расчета переменных Х в вычислительном алгоритме должен быть таким, чтобы на очередном i-ом шаге правые части расчетных соотношений были определены. С учетом этого вычислительный алгоритм имеет вид:

k=1.8 R₀,с-заданы

Перед началом расчетов необходимо задать (в соответствии с п.6 задания).R₀=0,2549; C=0,9162 – произвольные числа для генератора случайной последовательности R_k. Первый шаг вычислений для i=1 (момент времени t=Dt=0,05) имеет вид:

и т.д. для i от 2 до 60.

Задание. для заданной структурной схемы и ее параметров методом 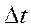рассчитать процесс изменения выхода системы y(t) на интервале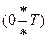

С использованием ЭВМ исследовать зависимость от заданного параметра системы при изменении этого параметра на 20% в обе стороны от заданного значения.

Дата добавления: 2015-07-25