Распределение Максвелла

Исходные данные:

1. Имеется большое, но конечное число молекул;

2. Скорости молекул различны ;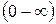

3. Движения молекул независимы друг от друга и молекулы обладают случайными энергиями.

Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергии и скорости отдельных молекул могут значительно отличаться от среднего значения.

Теория вероятностей позволяет определить долю молекул 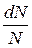, скорости которых заключены в интервале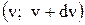

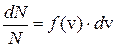– функция распределения (1)

где 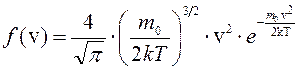, (2)

обозначения:

N – общее число молекул газа,

dN – число молекул, скорости которых заключены в определенном интервале,

v – нижняя граница интервала скоростей,

dv – величина интервала скоростей,

k = 1,38*10^–23 Дж/К – постоянная Больцмана,

е=2,718…

m₀ – масса молекулы.

Закон распределения Максвелла запишется в следующем виде:

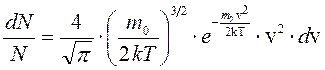(3)

График функции распределения f(v)

f(v)

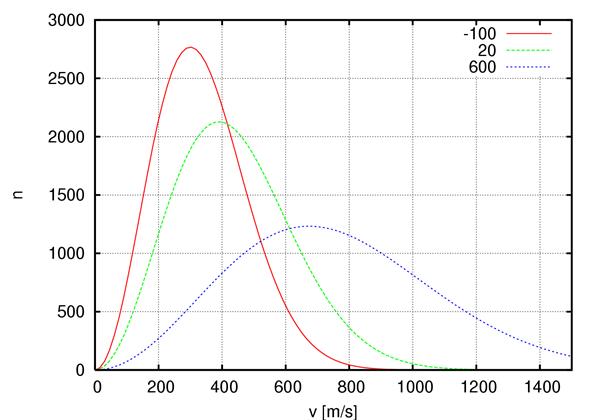
Площадь функции f(v) в интервале скоростей численно равна доле молекул, скорости которых заключены в интервале скоростей 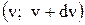. Площадь функции f(v) по всему интервалу скоростей всегда равна 1.

Из графика видно, что с ростом температуры газа пик функции смещается вправо и становится меньше.

Распределение Максвелла справедливо для частиц:

– не находящихся в силовом поле

– движения частиц- независимые

– подчиняются законам статистической механики.

Дата добавления: 2015-07-25