Анализ зависимости наиболее вероятной скорости молекул от температуры для данного газа.

Выберите одно из соединений. Установите во второй строчке его молярную массу. Проведите анализ зависимости v _в от температуры в пределах того диапазона температур, которые указаны в Таблице 1. Диапазон разделите так, чтобы получилось 5 точек. Результаты запишите в Таблицу 4. Извлеките и вычислите отношение .

Таблица 4

Соединение (укажите какое)	Температура t
Наиболее вероятная скорость v в
отношение

3. Расчет наиболее вероятной скорости (v_в), средней квадратичной и средней арифметической скорости молекул азота. Определение доли молекул обладающих этими скоростями.

По формулам (4, 5, 6) вычислите скорости , молекул азота для температуры t= 300 К. Результат занесите в Таблицу 5.

Проверьте условие нормировки функции (3*) для молекул азота, то есть возьмите интеграл в интервале скоростей, приведенном на графике функции распределения. (Предварительно введите параметры μ=28·10^-3 , t=300). Нижний предел интегрирования установите равным 1. Результат запишите в Таблицу 5.

Используя рассчитанные значения скоростей, путем интегрирования определите доли молекул, имеющих скорости v _в ± Δ v; ± Δ v; 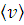± Δ v (где Δ v =5м/с). Для этого в формулу интеграла надо подставить нижний предел v -5 и в верхний v +5. Результат округлите до третьей значащей цифры и запишите в Таблицу 5.

Таблица 5

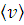
v в			Условие норми-ровки	v в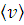±ΔV	±ΔV	±ΔV
Значение интеграла в пределах диапазона скоростей (*10­­­­­­­­^-2)

Путем интегрирования определите относительное число молекул азота, которые имеют скорости, отличающиеся от v _в в различных интервалах, указанных в Таблице 6.

Таблица 6

Интервал скоростей	Числовые значения интервала скоростей	%
1 - 0,5∙ v в
(0,5 - 1)∙ v в
(1 - 1,5)∙ v в
(1,5 - 2)∙ v в
(2 - 3)∙ v в
(3 - 5)∙ v в
(5 - 10)∙ v в

Из полученных данных определите:

a) Сколько процентов молекул имеют скорости, отличающиеся от v _в не более чем на 50%.

б) Найдите отношение доли молекул, определенных в пункте а) к доли молекул, скорости которых более чем в 5 раз превышают наиболее вероятную скорость. Результаты укажите в Таблице 7.

Таблица 7

Данные расчета пункта а)	Данные расчета пункта б)

4. Сопоставление результатов расчетов, полученных с использованием калькулятора и путем интегрирования.

Воспользовавшись формулами (4) и (7), рассчитайте с помощью калькулятора долю молекул азота при температуре Т = 300 К, обладающих скоростями в интервале от v до v +Δ v. Интервал скоростей приведен в таблице 8.

Таблица 8

№ варианта	Интервал скоростей (м/с)	№ варианта	Интервал скоростей (м/с)
	100 - 110		200-210
	150-160		102 - 112
	300-310		155-165
	395-405		300-310
	190-200		295-305
	110-120		190-200
	115 - 125		150-160
	155-165		340-350
	335-345		375-395
	345 - 355		195-205
	192-202		170-180
	108 - 118		285-295
	109-119		158-168
	364-374		300-310
	390-400		393-403
	190-200		100 - 110

Для удобства результаты промежуточных расчетов и окончательный результат занесите в таблицу 9. Проведите расчет с помощью интегрирования в этом же интервале скоростей. Результат запишите в таблицу. Оцените погрешность расчетов, проведенных двумя методами.

Таблица 9

Числовое значение интервала скоростей	Vв	U^2		ΔU	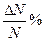(калькулятор)	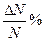(интеграл)

Вопросы

1) Какой физический смысл абсолютной температуры Т и универсальной газовой постоянной R?

2) Как влияет давление и объем газа на распределение молекул по скоростям?

3) Чему соответствует наиболее вероятная скорость молекул на графике функции распределения?

4) Получите из функции распределения молекул по скоростям функцию распределения по энергиям.

5) Исходя из функции распределения молекул по скоростям (формула 2), выведите закон, выражающий распределение молекул по относительным скоростям U (U= ) (формула 7).

---

Дата добавления: 2015-07-25