
|
Читайте также: |
Лекция 1.
Образование проекций
Метод проекций
Проекции центральные и параллельные.
Метод Монжа. Инвариантные свойства проецирования.
Проекции центральные
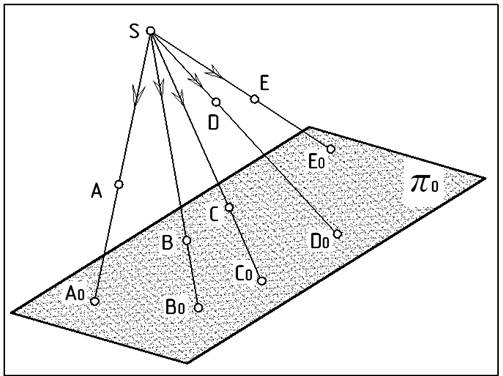
Рис.1.
Образование центральных проекций точек A, B, C, D, E, …
В основе центрального проецирования лежат полученные изображения точек (A B C D E…) на плоскости проекций π0
 (рис.1.) путем проведения проецирующих прямых (SA0, SB0, SC0, SD0, SE0, …) из центра проекций S через эти точки до пересечения с плоскостью проекций π0. В результате получаем центральные проекции точек (A B C D E …) на плоскости π0, а именно, A0, B0, C0, D0, E0, ….
(рис.1.) путем проведения проецирующих прямых (SA0, SB0, SC0, SD0, SE0, …) из центра проекций S через эти точки до пересечения с плоскостью проекций π0. В результате получаем центральные проекции точек (A B C D E …) на плоскости π0, а именно, A0, B0, C0, D0, E0, ….
Рис.2.
Образование центральных проекций кривых линий, принадлежащих проецирующей поверхности
[S A0 B0 C0 D0 E0 … ]
Очевидно, что проекции нескольких линий:
A1 B1 C1 D1 E1, …, A2 B2 C2 D2 E2, …, лежащих на поверхности S A0 B0 C0 D0 E0… (рис.2), будут проецироваться в одну линию A0 B0 C0 D0 E0… на плоскость проекций π0, где точки A0, B0, C0, D0, E0, … являются центральными проекциями точек A1 , B1 , C1 , D1 , E1, …, A2 , B2 , C2 , D2 , E2, …, на плоскость π0.
Проекции параллельные
Условимся считать, что все проецирующие прямые параллельны заданному направляющему вектору «S» (рис.3.).

Рис.3. Образование параллельных проекций точек
A, B, C, D, D1, D2
Проецирующие прямые AA0, BB0, CC0, DD0, D1D0, D2D0
параллельны заданному направлению проецирования «S».
Построенные таким образом проекции точек называются параллельными. Следовательно, параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению «S»,
с плоскостью проекций π0.
В параллельных проекциях, так же как и в центральных, для прямой линии проецирующей поверхностью в общем случае служит плоскость, и поэтому прямая линия вообще проецируется в виде прямой. При этом каждая точка и линия пространства имеют единственную проекцию.
Каждая точка на плоскости проекций может быть проекцией множества точек, если через них проходит общая для них проецирующая прямая, например, на рис.3. точка D0 служит проекцией точек D, D1 и D2.
Каждая линия на плоскости проекций может быть проекцией множества линий (рис.4), если они расположены в общей для них проецирующей плоскости.

Рис.4. Образование параллельных проекций линий,
расположенных в одной проецирующей плоскости AB B0A0.
«S» ― направление проецирования.
Проецирующие прямые AA0, BB0 параллельны заданному направлению проецирования «S».
На рис.4. отрезок A0B0 служит проекцией отрезка прямой AB и отрезков плоских кривых линий A1B1 и A2 B2.
Для единственного решения необходимы дополнительные условия.
Для построения проекций прямой достаточно спроецировать две точки и через полученные проекции этих точек провести прямую линию (рис.5).

Рис.5. Образование параллельных проекций прямых линий.
«S» ― направление проецирования.
Прямая AB параллельна направлению проецирования «S».
Прямая CD параллельнаплоскости проекций π0.
Точка «К» принадлежит прямой общего положения JT.
Проецирующие прямые AA0, BB0, CC0, DD0, JJ0, TT0, KK0 параллельны заданному направлению проецирования «S».
Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой, например, на рис.5. точка «К» принадлежит прямой, проекция К0 принадлежит проекции этой прямой.
Если прямая параллельна направлению проецирования (на рис.5., прямая A B), то проекцией прямой и любого ее отрезка является точка A0, она же B0. Отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину. На рис.5. C D = C0 D0 как отрезки параллельных прямых.
Параллельныепроекции делятся на прямоугольные и косоугольные.
В первом случае направляющий вектор «S» перпендикулярен плоскости проекций, а во втором расположен к плоскости проекций под острым углом.
В дальнейшем, в данном методическом пособии будем использовать только прямоугольные проекции.
Дата добавления: 2015-07-25; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Секрет очарования: «психический вирус»! | | | Лекция 2. |