|
Читайте также: |
В этой лекции все примеры даются только в рамках систем двух и трех взаимно-перпендикулярных плоскостей проекций.
Точка и прямая
2.1 Точка в системе двух взаимно перпендикулярных (ортогональных) плоскостей проекций π1, π2
Рассмотрим систему ортогональных плоскостей проекций (π1, π2) (рис.6.). Вертикальная плоскость (π2)называется фронтальной плоскостью проекций, а горизонтальная плоскость (π1) называется горизонтальной плоскостью проекций.
Построим в полученной системе (π1/π2) (рис. 6.) проекции точки «A». Для этого через точку «A» проведем две проецирующие прямые (A А ’ и A A ’’), перпендикулярные каждой из плоскостей проекций (π1 и π2). В результате получим горизонтальную проекцию точки «А», которую обозначим – (А ’) и фронтальную проекцию точки «А», которую обозначим – (A ’’).
Линия пересечения плоскостей π1 и π2 называется осью проекций. В дальнейшем эту ось будем обозначать буквами «XO» или дробью (π1 / π2) .
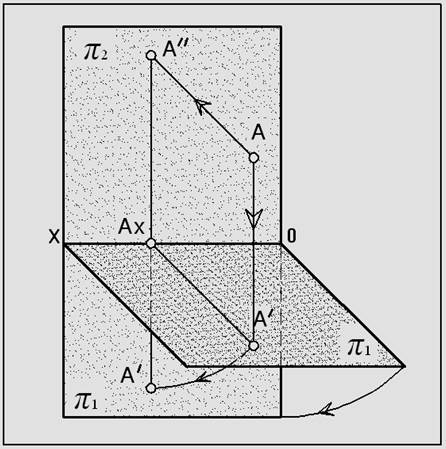
Рис.6. Образование чертежа
методом совмещения плоскостей проекций
В каждой из плоскостей проекций (π1 и π2) проводим через проекции – (А ’ и A ’’ ) вспомогательные прямые
(А ’ A x и A ’’ A x ), перпендикулярные оси проекций «XO».
Вращаем горизонтальную плоскость проекций (π1) вокруг оси «XO» до ее совмещения с фронтальной плоскостью проекций (π2).
В результате проекции (А ’ и A ’’ ) точки «A» располагаются на одной вертикальной прямой (А ’ A ’’ ), пересекающей ось «XO» в точке «A x ».
Если проведем обратное построение, то есть по двум проекциям восстановим положение точки в пространстве, то увидим, что две проекции точки определяют её положение в пространстве относительно данной системы плоскостей проекций.
На основе рис.6. выполняется изображение, показанное на рис.7.
Это изображение точки (в системе двух ортогональных плоскостей проекций) известно под названием «Эпюр Монжа».
Часто применяют в решении задач более простое изображение «Эпюра Монжа» для точки, которое показано на рис.8.
Прямую (А ’ A ’’), перпендикулярную оси проекций, Монж назвал - «линией связи».
Отрезок линии связи │A ’’ A x │ определяет расстояние от точки «A» до горизонтальной плоскости проекций (π1) – отрезок │а│.
Отрезок линии связи │А ’ A x │ определяет расстояние от точки «A» до фронтальной плоскости проекций (π2) – отрезок │b│.
Отрезок линии связи │ A ’’ A x │ определяет расстояние от точки «A» до горизонтальной плоскости проекций (π1) – модуль координаты «z».
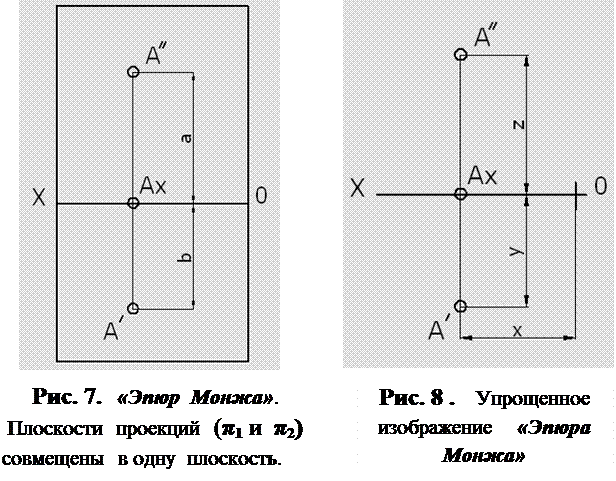
Отрезок линии связи │А ’ A x │ определяет расстояние от точки А до фронтальной плоскости проекций (π2) – модуль координаты «y».
Отрезок линии связи │ A x O│ определяет расстояние от точки «A» до профильной*) плоскости проекций (π3) – модуль координаты «x».
*) См. далее параграф 2.2 «Точка в системе трех взаимно перпендикулярных плоскостей проекций π1, π2, π3».
2.2 Точка в системе трех взаимно перпендикулярных (ортогональных) плоскостей проекций π1, π2, π3
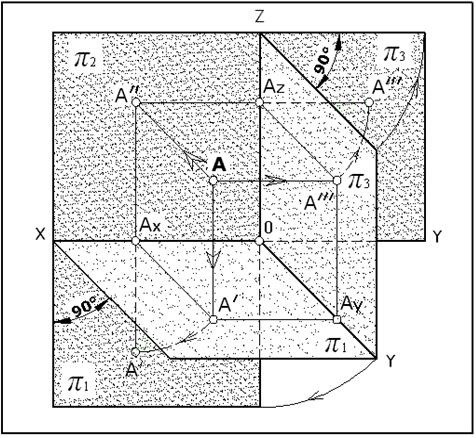
Рис.9. Это изображение точки (в системе трех ортогональных плоскостей проекций, совмещенных в одну плоскость) будем называть также «Эпюр Монжа».
Плоскость π3 ( рис.9.) перпендикулярна двум ранее рассмотренным плоскостям проекций π1 и π2 (рис.6.). Следовательно, плоскость π3 перпендикулярна оси проекций «XO».
Плоскость π3 пересекает плоскость π2 по линии «YO»,
а плоскость π3 по линии «ZO». Прямые «YO» и «ZO» также,
по аналогии с «XO», называют осями проекций.
Совмещаем плоскости проекций π1, π2, π3 с системой плоскостей координат.
В этом случае с осями проекций (XO, YO, ZO) будут совмещены также и оси координат (OX OY OZ).
Общую точку осей проекций «O» будем считать началом координат.
На основе рис.9. выполняется построение изображения, показанного далее на рис.10.
Рис. 10. Изображение точки в системе трех ортогональных плоскостей проекций, совмещенных в одну плоскость.
Прямые (А ’ A ’’) и (А ’’ A ’’’) перпендикулярные осям проекций, будем также называть «линиями связи».
Отрезок линии связи │A ’’ A x │= (a) определяет расстояние от точки «A» до горизонтальной плоскости проекций (π1).
Отрезок линии связи │A ’ A x │= (b) определяет расстояние от точки «A» до фронтальной плоскости проекций (π2).
Отрезок линии связи │A ’ A y ││= (c) определяет расстояние от точки «A» до профильной плоскости проекций (π3). Проецирование точки в системе трех взаимно - перпендикулярных (ортогональных) плоскостей проекций.
Часто применяют в решении задач более простое изображение – «Эпюр Монжа» для точки, которое показано на рис.11.
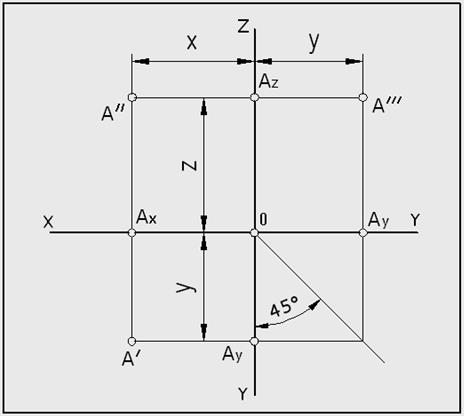
Рис. 11. Изображение точки в системе трех
ортогональных плоскостей проекций.
Отрезок линии связи │A ’’ A x │ определяет расстояние от точки «A» до горизонтальной плоскости проекций (π1) – «отрезок z».
Отрезок линии связи │A ’ A x │ определяет расстояние от точки «A» до фронтальной плоскости проекций (π2) – «отрезок y».
Отрезок линии связи │A ’ A y │ определяет расстояние от точки «A» до профильной плоскости проекций (π3) – «отрезок x».
Первая координата (x) точки А (отрезок Ax O) называется абсциссой.
Вторая координата (y) точки А (отрезок Ax А′) называется ординатой.
Третьякоордината (z) точки А (отрезок Ax A ′′) называется аппликатой.
То есть мы получили в распоряжение декартову систему прямоугольных координат.
Дата добавления: 2015-07-25; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проекции параллельные | | | Прямоугольных координат |