
|
Читайте также: |
Цель работы. Показать практическое применение метода моделирования для изучения динамики газовой струи при истечении ее в расплав.
Краткие сведения. Во многих металлургических процессах встречается подача газа в виде струй в слой расплава. К таким процессам относятся конвертирование штейнов, фьюмингование, огневое рафинирование, плавка с погруженным факелом и ряд других.
Во всех этих случаях условия протекания процесса, механизм его массообмена и теплообмена в слое расплава во многом определяются динамическими характеристиками газовой струи, поступающей в расплав.
Рассмотрим наиболее типичный случай процесса, протекающего при струйной подаче дутья в слой расплава - работу горизонтального конвертера.
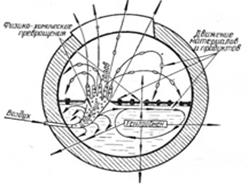
Рис 1. Схема работы конвертера
На рис. 1 приведена схема работы конвертера. По этой схеме видно, что размещение зон физико-химических и тепловых процессов, условия циркуляции ванны, условия службы огнеупорной кладки определяются динамикой газовой (в данном случае воздушной) струи, поступающей в конвертер.
Наиболее важной характеристикой струи для варианта погруженной подачи дутья является величина осевого проникновения струи в расплав. Теоретическим путем определить эту величину не представляется возможным, нет математического уравнения, описывающего закономерность распространения газовой струи в слое жидкости. Непосредственные замеры в струе в ванне конвертера также выполнить невозможно из-за недоступности струйного участка для наблюдений.
Единственным методом, с помощью которого можно получить представление о закономерностях распространения газовой струи в слое расплава, является метод моделирования.
Проникновение газовой струи в слой жидкости при погруженной подаче дутья определяется, в основном, соотношением сил инерции струи и сил всплытия газового факела из глубины слоя жидкости.
В качестве безразмерной величины, характеризующей это соотношение, академик М.В. Кирпичев предложил использовать вариант критерия гидромеханического подобия, названный критерием Архимеда:
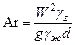
| (1) |
где W - скорость истечения газа, м/с; 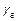 и
и  - удельный вес газа в струе и жидкости, кгс/м3; d - диаметр отверстия, из которого выходит струя, м; g – ускорение свободного падения, м/с2.
- удельный вес газа в струе и жидкости, кгс/м3; d - диаметр отверстия, из которого выходит струя, м; g – ускорение свободного падения, м/с2.
При высоких скоростях истечения газа, которые наблюдаются в фурмах конвертеров, процесс истечения газа можно рассматривать как адиабатический, пренебрегая теплообменом между струей и окружающим пространством.
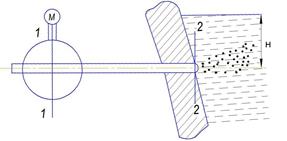
Рис. 2. Схема работы фурмы
Если рассматривать газ как идеальный, пренебрегая потерями напора, то уравнение Бернулли при истечении газа через фурму в расплав (рис. 2) для сечений 1- 1 и 2-2 можно записать так:
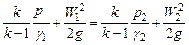
| (2) |
где k - коэффициент адиабаты (для воздуха k = 1,4); p 1, p 2- давления воздуха в сечениях 1-1 и 2-2, кгс/м2;  - удельные веса воздуха в сечениях 1-1 и 2-2, кгс/м3; W 1, W 2- скорости воздуха в сечениях 1-1 и 2-2; g - ускорение свободного падения, м/с2.
- удельные веса воздуха в сечениях 1-1 и 2-2, кгс/м3; W 1, W 2- скорости воздуха в сечениях 1-1 и 2-2; g - ускорение свободного падения, м/с2.
Полагая, что W2>>W1 т.к. F2<<F1 получим:
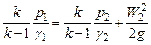
| (3) |
Параметры газа в коллекторе конвертера (p 1, 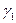 ) известны, т.к. на нем установлен манометр (в сечении 1- 1); выразим через них удельный вес газа в истекающей струе
) известны, т.к. на нем установлен манометр (в сечении 1- 1); выразим через них удельный вес газа в истекающей струе 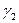 .
.
Для адиабатического процесса
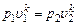 или или 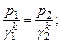
| (4) |
где υ -удельный объем, величина обратная удельному весу (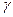 ), м3/кгс.
), м3/кгс.
Из формулы (4):
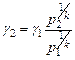
| (5) |
Подставив (5) в (3) получим:
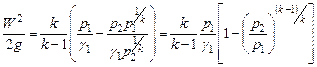
| (6) |
Далее выразим скорость истечения газа:
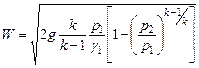
| (7) |
Для учета потерь энергии при истечении вводится коэффициент скорости:
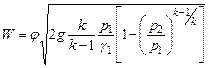
| (8) |
Подставив выражение скорости в критерий Ar (1) получим:
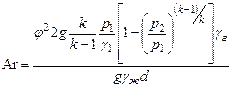
| (9) |
Заменив 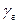 , на
, на 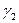 , используя формулу (5) и проведя преобразования, найдем:
, используя формулу (5) и проведя преобразования, найдем:
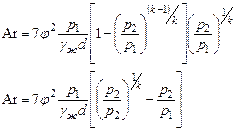
| (10) |
Для конвертеров цветной металлургии, перерабатывающих штейны, значения всех величин, входящих в формулу (10) могут быть заданы.
Пусть  = 5000 кгс/м3,
= 5000 кгс/м3, 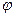 =0,9, d = 41 мм.
=0,9, d = 41 мм.
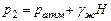
| (11) |
где р атм - атмосферное давление (пусть 10000 кг/м2); H - глубина погружения фурм в расплав (0,6 м); тогда р 2 = 13000 кгс/м2.
Задаваясь разными значениями давления воздуха на коллекторе (в сечении 1-1), характерными для горизонтальных конвертеров, построим график 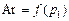 (рис. 3).
(рис. 3).
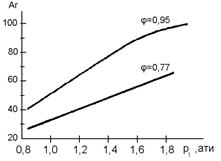
Рис. 3. Значения критерия Архимеда для фурм горизонтального конвертера
Расчеты показывают, что рабочие значения критерия Архимеда для конвертера находятся в зависимости от давления дутья в интервале 40 - 100. В таком диапазоне значений 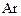 необходимо выполнить и опыты моделирования.
необходимо выполнить и опыты моделирования.
Описание установки. Схема установки для моделирования приведена на рис. 4.
В качестве жидкости, моделирующей расплав (штейн) используется вода ( = 1000 кгс/м3). Диаметр выходного отверстия фурменной трубки d = 7∙10-3 или d = 5∙10-3 м.
= 1000 кгс/м3). Диаметр выходного отверстия фурменной трубки d = 7∙10-3 или d = 5∙10-3 м.
Рассчитаем скорость воздуха, необходимую для получения рабочих значений критерия Архимеда (40 -100).
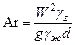
| (12) |
Отсюда
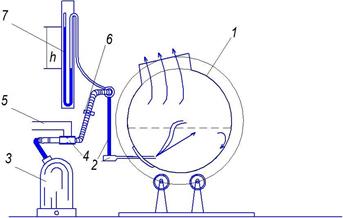
Рис. 4. Схема установкидля моделирования конвертера:
1 – модель; 2 – фурменное устройство; 3 – воздуходувка; 4 – диафрагма; 5 – трубки к микроманометру; 6 – зажим; 7 – манометр
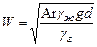
| (13) |
Для Ar = 40 при  = 1000 кгс/м3 и d =
= 1000 кгс/м3 и d = 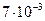 м
м
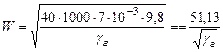
|
Поскольку γ г всегда больше единицы, W < 51,13 м/с.
Для Ar = 100
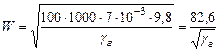
|
т.е. W < 82,6 м/с.
Определим давление, необходимое для создания скорости до 82,6 м/сек. Полагая, что эти скорости могут быть достигнуты при низких давлениях, воспользуемся простейшими формулами, полученными из уравнения Бернулли для несжимаемых жидкостей:
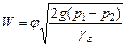 Откуда
Откуда 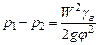
| (14) |
Приняв 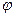 =0,9, получим
=0,9, получим
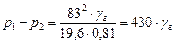 , кгс/м2 , кгс/м2
|
Допустим, что 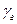 =
= 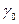 = 1,29 кгс/м3, тогда (р 1 – p 2) = 550 кгс/м2. Если
= 1,29 кгс/м3, тогда (р 1 – p 2) = 550 кгс/м2. Если 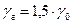 , тогда (p 1 - p 2) = 825 кгс/м2.
, тогда (p 1 - p 2) = 825 кгс/м2.
Если моделирование вести при Н = 80 мм вод. ст., то для рассматриваемых случаев:
р 1 = 630 мм вод. ст. (кгс/м2)
р 1 = 905 мм вод. ст. (кгс/м2)
Т.е. истечение происходит при сравнительно низких давлениях (меньше 1000 кгс/м2), для таких условий допустимо пренебречь разницей удельных весов газа перед выходом из фурмы и в струе, следовательно можно принять, что
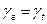
где 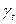 - удельный вес газа при температуре, которую он имеет в фурме (и струе).
- удельный вес газа при температуре, которую он имеет в фурме (и струе).
Для воздуха при t = 30° 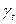 =1,16 кгс/м3. Температура 30° принимается в связи с тем, что воздух из фурмы модели поступает слегка подогретым за счет сжатия его на турбинах воздуходувного устройства.
=1,16 кгс/м3. Температура 30° принимается в связи с тем, что воздух из фурмы модели поступает слегка подогретым за счет сжатия его на турбинах воздуходувного устройства.
Для низких давлений истечения скорости струи может быть выражена формулой:
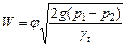
| (15) |
Подставив это выражение в формулу критерия Архимеда, получим для условий моделирования при 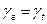 и
и  кгс/м3
кгс/м3
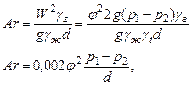
| (16) |
При 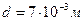
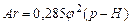
| (17) |
При 
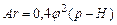
| (18) |
Порядок выполнения работы
А). Предварительные измерения.
1. Ознакомиться с инструкцией, разобраться в схеме установки (см. рис. 4), проверить работу всех ее элементов.
2. Не заполняя модели водой, включить воздуходувку (электропылесос) и снять несколько (2-3) значений р по манометру (9) (кгс/м2), и значений Δ Н по микроманометру.
3. Рассчитать теоретическое количество воздуха, которое пройдет через отверстие диаметром d = 7 мм или 5 мм при измеренных значениях давления по формуле:
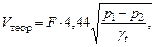 м3/с м3/с
| (19) |
где F - площадь отверстия, м2.
Опыт производить при режиме свободного истечения, т.е. при H = 0 и 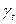 =1,2 кгс/м3, следовательно,
=1,2 кгс/м3, следовательно,
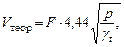 м3/с м3/с
|
Определить практический расход воздуха через фурму по измеренным значениям 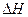 .
.
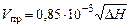 , м3/с , м3/с
| (20) |
Вычислить значение коэффициента 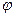 по формуле:
по формуле:
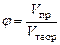
| (21) |
Результаты измерений и вычислений занести в таблицу 1:
Таблица 1
| № опыта | Измерения | Вычисления | |||
| p, мм вод. cт. | Δ Н, мм вод. ст. | V np, м3/с | V тeop, м3/с | 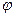
| |
Среднее значение 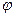
|
Б). Измерения по динамике струи.
Заполнить модель водой до такого уровня, при котором глубина погружения фурм составит 80 мм (заполнение водой производить при повернутой модели, чтобы не залить фурм).
Изменяя с помощью зажима (6) подачу воздуха в модель, измерять давление дутья р, мм вод. ст. и длину струи L, мм.
Опыт произвести для давлений: 100, 200, 300, 600, 800 мм вод. ст.
Отсчет давлений производить тщательно, с точностью ±1,0 мм вод. ст. Результаты измерений занести в таблицу 2.
Таблица 2
| № опыта | Давление р, мм вод. ст. | Противодавление Н, мм в cm | Проникновение струи L, мм |
На основании полученных данных произвести следующие расчеты:
1. Определить значения критерия Архимеда для каждого из давлений по формуле (17), используя найденное опытом значение коэффициента 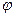 .
.
2. Определить критерий проникающей способности струи по формуле:
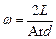
|
Из полученных результатов составить таблицу 3
Таблица 3
| Ar | |||||||||
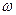
|
и построить график 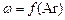
В) Перенос результатов моделирования на объект (образец).
1. Задавшись несколькими значениями давления дутья на конвертер (0,7; 1,2; 1,7 ати) по графику (рис. 3) найти соответствующие значения критерия Архимеда Arобр.
2. По экспериментальной кривой 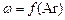 , полученной на модели определить значения
, полученной на модели определить значения 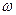 , соответствующие величинам Arобр.
, соответствующие величинам Arобр.
3.Определить осевое проникновение воздушной струи в слой штейна (т.е. в условиях образца) по формуле:
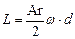
| (21) |
(если d - в мм, то и L - в мм, d принять равным 41 мм).
4. Построить график L = f(p) для условий образца.
Дата добавления: 2015-07-25; просмотров: 190 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ВВЕДЕНИЕ | | | В БАРАБАННОЙ ПЕЧИ |