эвольвентной зубчатой передачи

Институт металлургии и машиностроения

Кафедра «Технологические процессы и оборудование

автоматизированных машиностроительных производств»

Геометрический расчет

эвольвентной зубчатой передачи

Расчётно-графическая работа по ТММ

Выполнил ст.

Группа

ИСХОДНЫЕ ДАННЫЕ.

Число зубьев колеса 1 - Z₁ =.

Число зубьев колеса 2 - Z₂ =.

Модуль m = мм.

Межосевое расстояние a _w=

Угол профиля исходного контура =20^◦.

Коэффициент высоты зуба h_a ^*= 1. Коэффициент радиального зазора С^*= 0,25.

ГЕОМЕТРИЧЕСКИЙ РАСЧЁТ. (линейные размеры в мм.)

1. Радиусы делительных окружностей (по которым измеряется шаг зубьев)

r₁ =0,5∙ m Z₁= =

_. r₂ =0,5∙ m Z₂ = =

2. Шаг зубьев по делительной окружности p= m ∙ = =

3. Радиусы основных окружностей (с которых образуется эвольвента зуба).

r _b1 =r₁ ∙Cos = =

r _b2 = r₂∙Cos = =. (Cos =Cos20^◦=0,93969)

4. Делительное межосевое расстояние (при коэффициентах смещения инструмента

x₁ = x₂=0)

a = r₁ + r₂ = =

5. Угол зацепления передачи (в градусах) α_w^◦=arcos((a∙ Cosα)/ а_w) =

=

6.Необходимый суммарный коэффициент смещения (для обеспечения заданного межосевого расстояния а_w)

Σx= (x₁ + x₂₎ =(Z₁+ Z₂ )∙(invα_w-invα)/(2tgα) =

= =.

tgα=tg20^◦=0,364 invα= tgα- (α^◦/57,3)=0,0149. invα_w= tgα_w- (α_w^◦/ 57,3)=.

7. Коэффициент смещения x₁ находим из условия отсутствия подрезания при нарезании

колеса 1. x₁= h_а^*∙ (z_min-z₁)/ z_min =

z_min=2h_а^*/Sin² α=17 - минимальное число зубьев,при котором отсутствует подрезание.

8. x₂ = Σx- x₁ =.

9.Передаточное отношение зубчатой пары i _1-2=z₂/z₁= =

10. Радиусы начальных окружностей (перекатываются друг по другу без скольжения)

r_w1= a _w /(1+ i _1-2)= =

r_w2= a_w - r_w1= =.

11. Радиусы окружностей впадин зубьев.

r_f1= r₁+(x₁- h_a ^*- С^*)∙ m = =

r_f2= r₂+(x₂- h_a ^*- С^*) ∙ m= =

12. Радиусы окружностей вершин зубьев

r_а1= r₁+(x₁+ h_a ^*) ∙ m= =.

r_а2= r₂+(x₂+ h_a ^*)∙ m = =.

13. Толщина зуба колеса по делительной окружности

s₁=0,5р+ 2x₁∙ m ∙ tg = =

s₂=0,5р+ 2x₂∙ m ∙ tg = =

14. Ширина впадины зуба по делительной окружности

e ₁=р- s₁ = =

e ₂=р- s₂= =

15. Профильный угол эвольвенты на окружности вершин

_а1^◦= arcos(r _b1 / r_а1)= = град

_а2^◦= arcos(r _b2/ r_а2)= = град ..

Проверка качества зацепления передачи

1.Подрезание зубьев отсутствует (рассчитан требуемый коэффицент смещения при нарезании колеса 1.

2. Проверка зубьев на заострение.

Условие отсутствия заострения: толщина зуба

на окружности вершин s_a ≥0,2 m. Проверку выполняем для колеса 1.

s_а1= r_а1 ∙((s₁ / r₁)-2(inv _a1- inv ))=

=

INV _a1= tg _a1-( _a1^◦/57,3)= =.

3. Проверка коэффициента перекрытия.

Коэффициент перекрытия показывает среднее число пар зубьев колёс, находящихся одновременно в зацеплении. Для нормальной работы зубчатой пары необходимо, чтобы в момент выхода из зацепления одной пары зубьев следующая пара уже вошла в зацепление.

Для этого коэффициент перекрытия должен быть больше 1. В прямозубой передаче есть только торцевое перекрытие зубьев и, соответственно, торцевой коэффициент перекрытия.

=(z₁∙( tg _a1- tg _w)+ z₂∙( tg _a2- tg _w) )/(2 )=

= =.

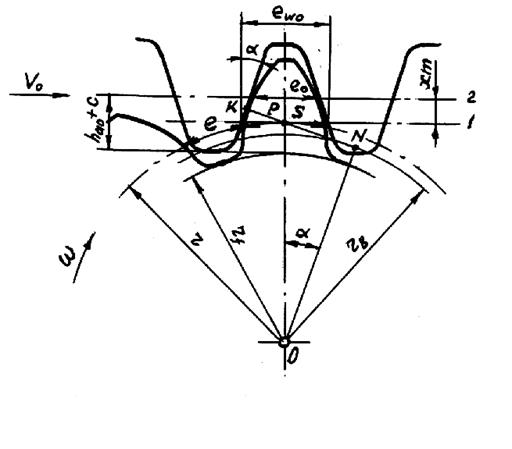
Эвольвентное зацепление

Схема станочного зацепления

Дата добавления: 2015-07-25