Для трех амортизаторов

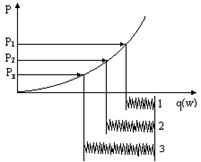
Если реакции лежат в одном диапазоне, то мы берем один и тот же тип амортизатора. Расчет ведем по минимальной деформации.

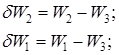
Если установлены разные амортизаторы, необходимо дополнительно учитывать при расчете толщины прокладки первоначальную разницу габаритных размеров и амортизаторов.

Динамический расчет

1. Определение инерционных и жесткостных параметров системы.

1.1 Определение инерционных параметров.

m_i масса – инерционный параметр системы при поступательном движении;

I_xx, I_yy, I_zz – моменты инерции при поворотном движении;

m – определяется суммирование масс различных частей, узлов, деталей блока.

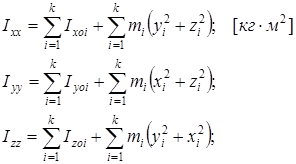
I_ii – собственный момент инерции всего блока относительного его центральных осей. Они определяются следующим образом:

– сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам.

– дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z.

1.2 Жесткостные параметры системы.

C_g – суммарная жесткость системы (динамическая).

Представляется в виде суммы динамических жесткостей системы или поворотных жесткостей.

Динамические жесткости амортизаторов определяются по графикам динамической жесткости.

Эти графики сняты экспериментально. А – амплитуда вибрации основания.

C_gu – значение динамических жесткостей.

Характер зависимости – линейный. График дается для трех значений: P_min, P_max, P_min. Зная график зависимости и амплитуду вибрации основания, можно говорить об определении значений динамических жесткостей амортизаторов. Если графика нет, то C_g = 1,1 … 1,2 C, где С – статическая жесткость, определяемая по графику статической жесткости.

Динамическая жесткость системы определяется только через динамические жесткости амортизаторов и не может быть изменена при выбранном типоразмере амортизатора. Поворотная жесткость определяется еще и координатами установки амортизатора и может быть изменена за счет изменения этих координат.

1.3 Определение парциальных частот.

Парциальные частоты определяются через инерционные и жесткостные параметры системы.

1.4 Определение собственных частот системы амортизации.

Собственные частоты системы амортизации определяются через парциальные частоты с учетом наличия плоскостей симметрии.

1.5 Расчет коэффициента динамичности.

- собственная частота;

- воздействующая частота;

m - масса блока;

k_g - коэффициент демпфирования, который определяется по графику (график экспериментальный для различных нагрузок на амортизатор);

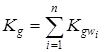- в закрытой области.

- сумма по всем амортизаторам по соответствующим индексам.

В зарезонансной зоне можно принять так: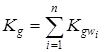

В резонансной зоне – очень сильная зависимость.

Для уменьшения коэффициента динамичности в резонансной зоне необходимо увеличить K_g. Для этого в системе предусматривается максимальная связность перемещений, т.е. отсутствие плоскостей симметрии.

1.6 Определение ускорения объекта.

Ориентировочно оценку коэффициента динамичности можно вести по АЧХ амортизатора.

Замечание: j_об – ускорение центра тяжести объекта. В некоторых точках блока за счет поворотных движений ускорение может быть больше.

Расчёт системы амортизации при ударном воздействии.

Воздействующий ударный импульс задаётся функцией ударного ускорения от времени. Импульс имеет произвольную форму, но при расчётах и испытаниях приняты следующие типовые формы импульсов:

1. прямоугольная форма; 2. косинусоидальная форма (пол-волны); 3. косинусоидальная форма (четверть волны); 4. треугольник любой формы;

Характер движения объекта при ударе определяется воздействующим ударным импульсом, массой объекта и ударными характеристиками амортизато­ров. Такими характеристиками являются:

	1. силовая ударная характеристика Fw(W) - зависи­мость ударной силы от деформации.
2. ударная энергоёмкость Пw(W) - определяет потен­циальную энергию амортизатора в зависимости от де­формации.

Связь между характеристиками такова: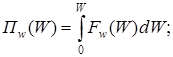

Для нормализованных амортизаторов приводятся обе указанные харак­теристики, снятые экспериментально, причем для различных направлении амор­тизаторов характеристики также будут различны.

Далее предположим, что удар направлен вдоль оси W.

Для расчёта системы строят суммарные ударные характеристики. Сумми­рование ударных характеристик производится по координатам. Далее в расчетах используются эти суммарные характеристики.

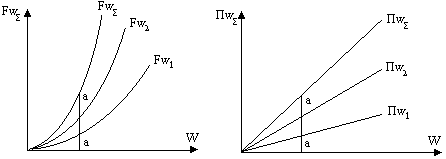
Движение блока при ударе

Предположим, что движение проходит по направ­лению W и вниз, т.е. блок падает на непод­вижную жёсткую платформу. Рассмотрим определён­ные стадии движения блока и энергетические со­отношения при этом.

№	Время	Приращение перемещения	Приращение скорости	Кинетическая энергия	Потенциальная энергия

1. В момент t₀ блок в положении равновесия.

2. Блок воспринимает удар; потенциальная энергия - функция от пере­мещения и определяется по графику.

3. Блок продолжает двигаться дальше до t₁, при котором приращение скорости равно нулю. При этом деформация амортизаторов максимальна.

Методики расчёта на ударные воздействия. (упрощённая и метод эквивалентных прямоугольных импульсов)

1. Упрощённая методика.

Здесь удар трактуется мгновенным. При этом принимают потенциальную энергию, определяемую деформацией равной нулю. . Следовательно, вся кинетическая энергия, за­пасённая за время удара, полностью переходит в потенциальную энергию максимально сжатых амортизаторов.

m – известна;

При заданной форме ударного импульса параметры системы и определяются следую­щим образом (при ):

Для типовых форм ударных импульсов формул для расчета и приводятся в соответствующих таблицах.

Методика определения ускорения объекта сводится к следующим действиям:

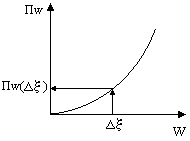
1. По ударной характеристике энергоёмкости системы (определяем максимальную деформацию амортизаторов:

2. По максимальной деформации, с помощью силовой ударной характеристики, определяем максимальную ударную силу: .

3. По максимальной ударной силе определяем ускорение объекта по формуле:

Этот алгоритм действителен и для метода эквивалентных прямоугольных импульсов.

Оценим погрешность этого расчёта:

знаменатель известен, числитель определяется то графику энергоемкости, т.к. значение известно.

Упрощённая методика.

Здесь удар трактуется мгновенным. При этом принимают потенциальную энергию, определяемую деформацией равной нулю. . Следовательно, вся кинетическая энергия, за­пасённая за время удара, полностью переходит в потенциальную энергию максимально сжатых амортизаторов.

m – известна;

При заданной форме ударного импульса параметры системы и определяются следую­щим образом (при ):

Для типовых форм ударных импульсов формул для расчета и приводятся в соответствующих таблицах.

Методика определения ускорения объекта сводится к следующим действиям:

4. По ударной характеристике энергоёмкости системы (определяем максимальную деформацию амортизаторов:

5. По максимальной деформации, с помощью силовой ударной характеристики, определяем максимальную ударную силу: .

6. По максимальной ударной силе определяем ускорение объекта по формуле:

Этот алгоритм действителен и для метода эквивалентных прямоугольных импульсов.

Оценим погрешность этого расчёта:

знаменатель известен, числитель определяется то графику энергоемкости, т.к. значение известно.

Дата добавления: 2015-07-11